Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Série geométrica

Ver Teoria
Exercício 38123456789101112131415161718192021222324252627282930313233343536373940414243

Enunciado

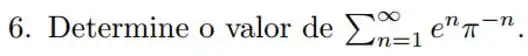
Passo 1

Primeiro, vamos escrever essa série de forma mais bonitinha:

∑ n = 1 ∞ e n π - n = ∑ n = 1 ∞ e π n

Passo 2

Caramba! Isso é uma série geométrica com r = e π . Lembra como é essa série?

∑ n = 0 ∞ r n = 1 1 - r

Com r < 1 . No nosso caso, lembre-se de que e ≅ 2,7 e π ≅ 3,14 . Logo, e π < 1 . Outro ponto importante: perceba que nesse somatório acima, o n começa em 0 . Na nossa série, ele começa em 1 . Vamos consertar isso assim:

∑ n = 0 ∞ r n = 1 1 - r

r 0 + ∑ n = 1 ∞ r n = 1 1 - r → 1 + ∑ n = 1 ∞ r n = 1 1 - r →   ∑ n = 1 ∞ r n = 1 1 - r - 1

Então, teremos:

∑ n = 1 ∞ e π n = 1 1 - e π - 1

Resposta

∑ n = 1 ∞ e π n = 1 1 - e π - 1

Exercícios de Livros Relacionados

Nos Exercícios 7-14, escreva os primeiros termos de cada série para mostrar como a série começa. Então, calcule a soma da série. ∑ n = 2 ∞ 1 4 n
Determine se a série geométrica é convergente ou divergente. Se for convergente, encontre sua soma. 3 - 4 + 16 3 - 64 9 + …
Determine se a série geométrica é convergente ou divergente. Se for convergente, encontre sua soma. ∑ n = 1 ∞ 3 n + 1 - 2 n
Determine se a série é convergente ou divergente expressando s n como uma soma telescópica. Se for convergente, encontre a sua soma. ∑ n = 2 ∞ 1 n 3 - n
Determine se a série é convergente ou divergente. Se for convergente, calcule sua soma.13- - 2 + 5 2 - 25 8 + 125 32 + …