Calcule , o limite, quando existir. Caso contrário, justifique.
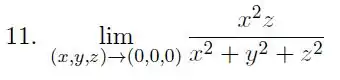
Passo 1
Vamos primeiro tentar substituir os valores :
E caímos numa indeterminação do tipo “”.
Passo 2
Bem, então vamos tentar aplicar o Teorema do Sanduíche! :)
Vamos dar uma olhada na expressão do limite:
A gente tem que limitar alguma coisa, criando uma inequação.
Dividindo tudo por :
Passo 3
Beleza, então essa expressão é limitada. E também temos que
Logo, pelo teorema do anulamento, diretamente temos que
Resposta
Exercícios de Livros Relacionados
Sabendo que cos 1 y ≤ 1 , você pode dizer algo sobre lim x , y → 0,0 x cos 1 y Justifique sua resposta.
Nos Exercícios 61-66, encontre o limite de f quando (x, y) → (0, 0) ou mostre que o limite não existe. f x , y = x 3 - x y 2 x 2 + y 2
Nos Exercícios 61-66, encontre o limite de f quando (x, y) → (0, 0) ou mostre que o limite não existe. f x , y = 2 x x 2 + x + y 2
Sabendo que sen 1 x ≤ 1 , você pode dizer algo sobre lim x , y → 0,0 y sen 1 x Justifique sua resposta.
Releia o Exemplo 5. Substitua m = tg θ na fórmula f x , y y = m x = 2 m 1 + m 2 E simplifique o resultado para mostrar como o valor de f varia de acordo com o ângulo de inclinação da retaUtilize a f