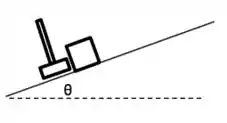
Um bloco de massa repousa sobre um plano inclinado de um ângulo em relação à horizontal. O bloco é subitamente impulsionando, paralelamente ao plano, por uma marreta, parando após percorrer uma distância no plano inclinado, a partir de sua posição inicial, como mostra a figura. Sabendo-se que o coeficiente de atrito cinético entre o bloco e o plano é , determine:
O trabalho realizado pela força de atrito durante o deslocamento ;
A velocidade do bloco, imediatamente após a marretada;
O valor do impulso que a marreta imprime o bloco.
Passo 1
Para determinar o trabalho realizado pela força de atrito, vamos relembrar a sua definição:
Onde é o ângulo entre o vetor força e o vetor deslocamento.
No caso, a força em questão é de atrito, então:
Como a força de atrito tem sentido contrário ao deslocamento, . Substituindo para determinar o trabalho, temos:
Passo 2
Para determinar a velocidade do bloco após a marretada, podemos usar o teorema do Trabalho e Energia Cinética:
Passo 3
Para determinar o impulso devemos lembrar da seguinte relação:
Resposta