Jason desliza em linha reta ao longo de uma superfície plana com seus esquis movidos a jato. A massa combinada de Jason e esquis é de (a massa do combustível é desprezível) e Jason parte do repouso. Devido ao funcionamento do motor é exercida uma força de sobre os esquis para impulsioná los. O coeficiente de atrito cinético entre os esquis e a água é de . Infelizmente, os esquis ficam sem combustível depois de apenas . O quão longe Jason viaja até finalmente parar?
A)
B)
C)
D)
E)
Passo 1
Fala aí!! Vamos entender o que está acontecendo aqui.
Temos 2 momentos; um quando o motor tá funcionando. E o outro é quando o motor para.
Então, as forças que atuam em cada situação são diferentes. Vamos analisar cada parte separadamente.
Bora!!!!
Passo 2
Primeiro, quando o motor tá funcionando, temos o peso, a normal, a força de atrito e a força F que o motor impulsiona:
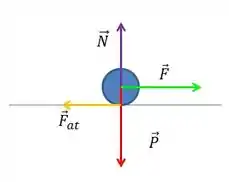
No eixo vertical a resultante é zero, então:
No eixo horizontal, temos uma aceleração, ou seja, uma força resultante:
Mas sabemos que:
Então:
Substituindo os valores, temos:
Agora vamos ver qual a distância que ele percorre nessa primeira parte do movimento.
Show!
Vamos calcular também qual é a velocidade que o Jason tem quando o motor para de funcionar. Pois essa será a velocidade inicial da parte 2.
Beleza! Vamos começar a analisar a parte 2 agora.
Passo 3
Então essa velocidade que a gente achou é a velocidade inicial da segunda parte do movimento. Onde a força F não atua mais.
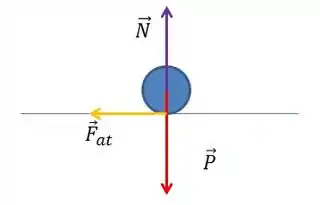
Nesse caso, teremos que:
(considerando o sentido positivo de x para a direita).
Então:
Show! Achamos a aceleração da segunda parte do movimento. Vamos ver o quanto ele anda até parar. Então a velocidade final é zero, e a inicial é aquela que a gente achou la no passo 1.
Vamos usar torricelli, porque não sabemos o tempo da segunda parte.
O é o queremos saber e o vai ser a distância que ele chegou no fim da primeira parte do movimento.
Substituindo os valores:
Resolvendo isso:
escrevendo o resultado com ordem de grandeza:
Que é a letra A!
Resposta
Alternativa A.