[Enunciado comum às Questões 5 e 6]
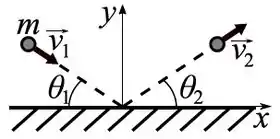
Uma bola de massa , movendo-se com velocidade colide com uma parede vertical, como mostra a figura abaixo. Depois da colisão, a bola tem velocidade . Os ângulos que os vetores e fazem com a parede são e , respectivamente. é o impulso exercido pela parede sobre o bloco durante a colisão.
[Questão 6]
Suponha agora que a bola possui uma massa . Os ângulos satisfazem e , enquanto que . O tempo de colisão é igual a . Qual é a força média que a parede exerce sobre a bola?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Quando a bola colide com a parede, a parede exerce uma força sobre a bola durante um certo intervalo de temp, ou seja, realiza um impulso sobre a bola que faz com que a direção da sua velocidade mude porém seu módulo se mantenha.
Mas por que estamos falando sobre impulso??
Bom, nosso objetivo é achar a força média sobre a bola na colisão, certo?
Então, existem duas relações que podemos fazer através do impulso que permitem a gente chegar nessa tal força média.
A primeira relação é o Teorema Impulso-Momento Linear:
Como temos as informações sobre as velocidades inicial e final e também a massa da partícula, conseguimos encontrar , ou seja, sabemos o impulso sobre a bola.
Além disso, sabemos que o impulso pode ser calculado através de:
Assim, como sabemos o tempo de duração da colisão, conseguimos encontrar a força média .
Mãos à obra, vamos fazer essas contas!
Passo 2
Vamos começar aplicando o Teorema Impulso-Momento Linear:
Passo 3
Vamos decompor esses vetores velocidade, para escrevê-los em suas componentes:
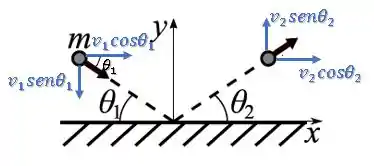
Então, temos que o Teorema fica assim:
Substituindo os valores, temos:
Aplicando o valor da massa:
Passo 4
Agora, basta usar a nossa segunda relação entre impulso e força resultante média:
Ficamos com a letra (e).
Resposta
Letra (e)