2) Um bloco de massa está ligado a uma mola de constante elástica e comprimento natural . O bloco é solto do repouso na posição e desliza para cima por uma haste lisa sob ação de uma força constante de módulo , que faz um ângulo com a vertical.
Adote para a aceleração da gravidade o valor .
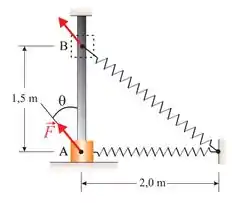
A velocidade do bloco na posição , em unidade do SI, é:
a)
b)
c)
d)
e)
Passo 1
Fala aí, galerinha! Tudo belezinha com vocês?
Bom, a questão deu pra gente um esquema onde uma mola está ligada a um bloco que está acoplado a uma haste e se movimenta por ela sob o efeito da força que a amola exerce. O que devemos encontrar é a velocidade do bloco quando ele está na posição . Para isso, vamos utilizar o teorema do trabalho e energia cinética, uma vez que o bloco chega até a posição devido a ação de uma força exercida pela mola.
Vamos extrair todas as informações necessárias para esse cálculo. Então vem comigo, que eu te ajudo.
Passo 2
Vamos começar lembrando que o teorema do trabalho energia cinética é dado por:
O trabalho envolvido nessa situação é devido a força Peso , força elástica e força . Com isso podemos escrever:
Como o bloco parte do repouso, podemos admitir . E teremos:
Passo 3
Outra coisa que podemos nos lembrar é que o trabalho da força elástica é dado por:
que será
Como já calculamos na questão 1 dessa prova, temos:
Assim,
Passo 4
E o trabalho da força Peso é dado por
E analisando melhor a figura, veremos que
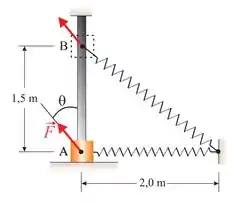
Passo 5
E o trabalho da força , será dado por:
Assim:
Passo 6
Agora basta substituirmos todas as informações que encontramos na relação:
E teremos:
Isolando , teremos:
E prontinho. Velocidade do ponto calculada.
Resposta
Resposta: a)