Uma esfera de massa é lançada em um trilho unidimensional de atrito desprezível com velocidade ao encontro de uma segunda esfera lançada simultaneamente de massa desconhecida com velocidade . As esferas colidem elasticamente e durante a colisão a primeira esfera sofre uma força dada pelo gráfico abaixo.
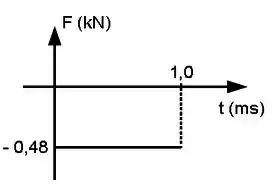
(d) Determine e os impulsos nas duas esferas
Passo 1
Momento linear é conservado?
Antes de mais nada, vamos primeiro lembrar o que é preciso pro momento linear ser conservado, beleza? Dá uma olhada:
Temos então duas formas de escrever a variação do momento linear e ela então vai ser quando não tivermos impulso e quando a força resultante externa for nula. Pro sistema (duas bolinhas), o enunciado não nos disse nada sobre impulso, não é mesmo? E ainda disse que a colisão foi elástica. Tá no papo então, o momento linear do sistema só pode ter se conservado! E, se é o caso, vale então:
Passo 2
Calcular a partir da análise gráfica
Olha que conveniente! O gráfico do enunciado é exatamente um gráfico de força por tempo! Podemos então calcular pelo gráfico, já que quem sofre a força do gráfico é a esfera ! Partindo pras contas, vamos ter: