UFRJ, Física 1, P2 2019.1, Questão 5 – Trabalho Impulso, Quantidade de Movimento e Conservação de Energia Mecânica
A figura mostra um carrinho de massa m, sobre um trilho de ar, que comprime de x uma mola de constante elástica k. O carrinho está inicialmente preso ao suporte do trilho por um fio. O fio é cortado, e a mola expande-se empurrando o carrinho. Ao passar pela posição de equilíbrio da mola, O, o carrinho perde contato com a mola. No trajeto até perder contato com a mola, o impulso fornecido ao carrinho foi
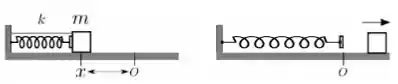
a)
b) 2
c)
d)
e)
Passo 1
Bom, como a gente já viu antes, o Impulso ele pode ser calculado pela variação da quantidade de movimento, certo? Então 𝐼=Δ𝑄, sendo 𝑄=𝑚𝑣. Como no início o bloquinho tá preso, não temos velocidade, então o impulso será simplesmente 𝐼=𝑄𝑓𝑖𝑛𝑎𝑙=𝑚𝑣𝑓𝑖𝑛𝑎𝑙, então a bronca da questão é encontrarmos a velocidade com que o bloco foi jogado pela mola! EITA!
Conservação de Energia Mecânica de novo! Dessa vez temos a Potencial Elástica e a Cinética! Pra gente descobrir essa velocidade, é so igualarmos a energia antes com a energia depois...
Passo 2
Agora que já temos nossa velocidade, podemos calcular o momento linear e assim encontramos o resultado do nosso Impulso! Então temos: 𝐼 = 𝑚𝑣 =
Xiiiii, não temos isso no gabarito Então vamos fazer umas alterações nessa expressão! Como o x tá elevado ao quadrado dentro da raiz quadrada, podemos tirá-lo dali
E, reacionalizando aquela raiz de x ali, a gente fica com
Tranquilasso? Fechouuuu?