UFF, Física 1, Prova 1, 2016.1
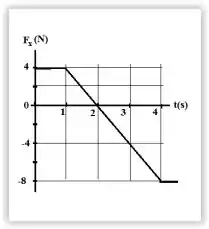
A figura representa a força sobre um corpo de massa igual a que está movendo-se ao longo do eixo. Se a velocidade do corpo é no instante , qual é a velocidade do corpo no instante ?
(A)
(B)
(C)
(D)
(E)
Passo 1
Sabemos que o impulso é dado pela área do gráfico de Força x Tempo. Descobrindo o impulso, podemos aplicar a relação dele com o momento linear:
Vamos começar pela área do gráfico então:
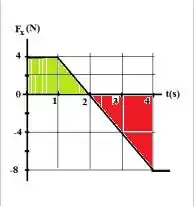
A parte verde é positiva e a vermelha negativa:
Área verde:
Área vermelha:
Assim chegamos que o impulso total no tempo de segundos vale:
Passo 2
Agora aplicamos a fórmula que relaciona o impulso com velocidade e massa:
Resposta
(C)
Exercícios de Livros Relacionados
Um carro de 1400k g está se movendo inicialmente para o norte a 5,3m / s , no sentido positivo de um eixo y . Depois de fazer uma curva de 90 ° para a direita em 4,6s , o motorista desatento bate em u
A pá de um taco de golfe segue se movendo para a frente após atingir a bola de golfe. O momentum da mesma é conservado na colisão? Explique, identificando claramente qual é o sistema.
Um objeto em repouso sobre uma superfície plana e horizontal explode dividindo-se em três fragmentos, um deles com massa sete vezes maior que a do outro. O fragmento mais pesado desliza por 8,2m até p
Em um teste balístico, uma bala de 25g desloca-se horizontalmente, a 1.200m / s , em direção a um alvo estacionário de 30c m de espessura e 350k g de massa e emerge do mesmo com velocidade de 900m / s
Força sobre uma bola de golfe. Uma bola de golfe de 0,0450k g que estava inicialmente em repouso passa a se deslocar a 25,0m / s depois de receber o impulso de um taco. Se o taco e a bola permaneceram