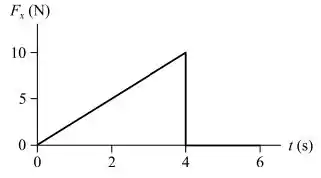
Um objeto de , inicialmente em repouso, é submetido à força variável dada na figura ao lado. Qual é a variação do momento linear do objeto entre e ?
(A)
(B)
(C)
(D)
(E)
Passo 1
O momento linear é dado por:
Lembra que quando não há forças externas, o momento linear se conserva?
Isso acontece justamente porque uma força faz o momento linear variar.
Assim, podemos descobrir a variação do momento linear em um intervalo de tempo, integrando a função da força:
Mas calma, não se asssuste com essa integral...
Podemos calcular a integral de uma função pela área abaixo do gráfico (nesse caso, um triângulo).
Passo 2
Queremos a variação entre os instantes e :
Isso resulta na área abaixo do gráfico entre e :
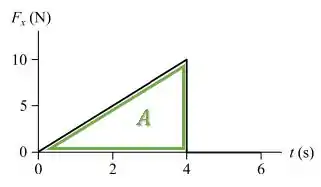
Ficamos com a alternativa (B).
Resposta
Letra (B)
Exercícios de Livros Relacionados
Um carro de 1400k g está se movendo inicialmente para o norte a 5,3m / s , no sentido positivo de um eixo y . Depois de fazer uma curva de 90 ° para a direita em 4,6s , o motorista desatento bate em u
A pá de um taco de golfe segue se movendo para a frente após atingir a bola de golfe. O momentum da mesma é conservado na colisão? Explique, identificando claramente qual é o sistema.
Um objeto em repouso sobre uma superfície plana e horizontal explode dividindo-se em três fragmentos, um deles com massa sete vezes maior que a do outro. O fragmento mais pesado desliza por 8,2m até p
Em um teste balístico, uma bala de 25g desloca-se horizontalmente, a 1.200m / s , em direção a um alvo estacionário de 30c m de espessura e 350k g de massa e emerge do mesmo com velocidade de 900m / s
Força sobre uma bola de golfe. Uma bola de golfe de 0,0450k g que estava inicialmente em repouso passa a se deslocar a 25,0m / s depois de receber o impulso de um taco. Se o taco e a bola permaneceram