UFSC, Araranguá, Física 1, P3 - 2021.2, Questão 2
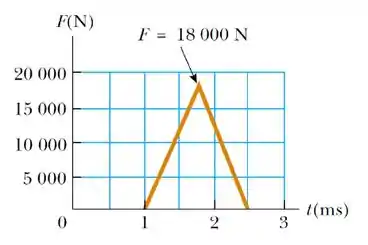
Em uma tacada de baseball, a força de interação entre o taco e a bola varia com o tempo de acordo com o gráfico ao lado. Desta curva, determine (a) o impulso fornecido à bola, (b) a força média exercida sobre a bola, e (c) a força máxima exercida sobre a bola.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu um gráfico de variação da força em função do tempo que descreve a tacada em uma bola de baseball.
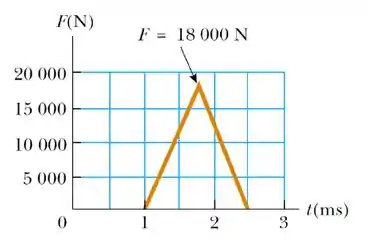
A gente precisa determinar o impulso fornecido a bola na letra a), a força média na letra b), e a força máxima exercida sobre a bola na letra c). Pra calcular o impulso, vamos que considerar a relação:
Como temos um triângulo, vamos calcular essa área multiplicando metade de sua altura por sua largura. No item b), para encontrar a força média, vamos dividir o valor do impulso pela variação de tempo. E verificar a força máxima no gráfico.
Vamos lá!
Passo 2
Vamos começar calculando a área sob a curva do gráfico, que é igual ao módulo do nosso impulso. Como temos um triângulo, vamos fazer:
Onde é a altura do triângulo e a sua largura. Olhando no gráfico, temos a altura:
E a largura:
Logo,
Passo 3
Na letra b), vamos calcular a força média exercida sobre a bola por meio da equação:
Onde é o impulso que nós calculamos no passo anterior e é a variação de tempo. Olhando o gráfico novamente, nós temos:
Substituindo tudo na equação:
Ou
A força máxima exercida sobre a bola é dada pela altura máxima da curva, mostrada no gráfico. Então, temos na letra c):
Ou
Prontinho, galera! Até a próxima! 😉
Resposta
a)
b)
c)