Uma corrente de densidade linear constante, comprimento e massa está sobre uma mesa horizontal cujo comprimento é ligeiramente inferior a de modo que uma pequena parte da corrente, de comprimento desprezível, fica pendurada. A parte da corrente que está sobre a mesa começa aos poucos a deslizar sem atrito. Pede-se calcular:

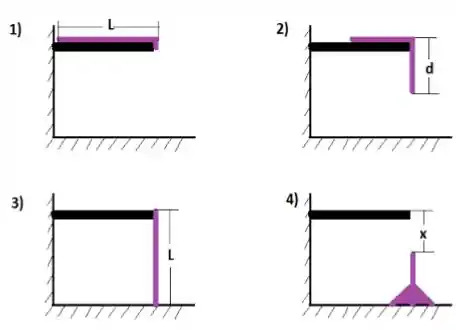
(a) o trabalho realizado pela força gravitacional quando o comprimento da parte pendurada atinge (item 2) da figura.

(b) a velocidade da corrente no instante em que a parte pendurada é igual a .

(c) a aceleração quando .

(d) Supondo agora que a corrente tenha escorregado completamente da mesa como mostra a figura acima (item 3), pede-se calcular a força exercida pelo solo sobre a corrente (força normal) após a corrente ter escorregado uma distancia igual a , como indicado pela figura acima (item 4). Suponha para tanto que a velocidade inicial com que a corrente começa a cair é nula.

Obs: Considere

(b)

Usando o teorema do trabalho e energia cinética, temos que o trabalho realizado pela força gravitacional vai ser igual a variação da energia cinética, visto que não tem atrito e portanto a energia mecânica é conservada. Ficará assim:

Lembrando que a energia cinética inicial é nula.

No item anterior já calculamos o trabalho da força gravitacional.

Substituindo os dados:

(c)

A aceleração pode ser calculada pela segunda lei de Newton, ou seja:

Lembrando que:

Substituido:

Substituindo os dados do problema:

(d)

A força exercida pelo solo é por definição igual a:

Entretanto, a massa da corda que está em contato com a corda corresponde a distância da figura 4, pois é este comprimento de corda que está enrolado no chão. Então:

Tanto a distância quando a velocidade dependem do tempo. Então temos que aplicar a regra do produto nessa derivada, ficará assim:

Entretanto, sabemos também que corresponde a velocidade, e que corresponde a aceleração, que no nosso caso é a gravidade. Então:

Porém temos pela fórmula:

Substituindo:

Logo temos que:

Substituindo os dados do problema: