Um corpo é arremessado diversas vezes em um plano horizontal sem atrito contra uma parede vertical, com a mesma energia cinética inicial, porém de uma posição diferente, a cada vez.

A figura mostra uma vista superior das trajetórias descritas pelo corpo em cada lançamento, designadas por , e .

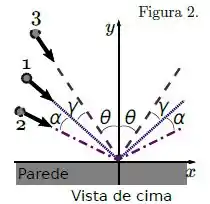
Sejam , e os impulsos produzidos pela parede sobre o corpo referentes às trajetórias , e respectivamente. Assinale a alternativa correta:

Ok, agora... pra que serve as expressões anteriores?

Bem, a razão é a seguinte. Se considerarmos a colisão como sendo totalmente elástica, nenhuma energia cinética é perdida, e por isso .

Como o impulso ao longo do eixo é zero, o módulo do impulso é . Mas quanto menor o ângulo que a partícula faz com a normal ao plano de colisão maior o valor do coseno (considerando ) e, consequentemente, maior o módulo do impulso.

Para cada caso, o ângulo seria:

Logo, teríamos o seguinte:

Que é a letra (d).

Só um probleminha no que fizemos antes: Em nenhum momento ele fala que a colisão é elástica. Bem, isso poderia ser um problema. Mas não é.

Esse terceiro passo é opcional, e ele não vai afetar a resposta final, só vai complementar o raciocínio anterior. Não precisa ler se não quiser!

Lembra que eu falei do ângulo com a normal que o corpo faz depois da colisão é igual ao ângulo antes da colisão? Bem, a figura do próprio enunciado nos diz a mesma coisa. Então valem as nossas fórmulas anteriores.

Além disso, como o corpo perde energia cinética, a velocidade final e a inicial são diferentes e .

O módulo do impulso então vai ser:

Abrindo os termos:

Agora, somando os dois e, lembrando que , temos:

A trigonometria tem algo muito importante a nos dizer, chamada coseno da soma.

O que significa que o módulo do momento fica:

E de novo, quando diminui, aumenta e o impulso aumenta. Quando aumenta, vai diminuindo, inclusive atingindo valores negativos.

O que nos diz que embora a equação tenha mudado, a resposta não mudou!