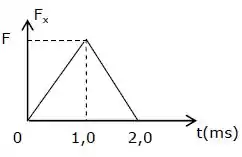
Dois blocos de massas e deslizam sem atrito sobre uma superfície horizontal. O bloco M desliza para leste com rapidez de e colide com o bloco m que desliza para oeste com rapidez de . Após a colisão os blocos ficam colados. O gráfico abaixo mostra a variação com o tempo do módulo da força exercida por um bloco sobre o outro durante a colisão. Qual é o valor de no gráfico?
(A)
(B)
(C)
(D)
(E)
Passo 1
Nessa questão vamos utilizar dois conceitos. O primeiro deles é que o impulso de uma força variável, como é o caso, é calculado por meio da integral da força no tempo:
E essa integral é igual a área abaixo do triângulo, que podemos calcular diretamente com:
OBS: O tempo está em milisegundos, por isso não podemos esquecer do .
Ok, beleza. Mas o que o ** tem a ver com as calças?

Bom, o enunciado nos deu informações sobre as massas e sobre as velocidades dos blocos antes e após a colisão. Então, podemos relacionar esses dados com o impulso a partir do teorema impulso-momento linear:
Ahhh, agora fez sentido.
Então, basta nós calcularmos a variação do momento linear em um dos dois blocos que conseguimos achar a força imbutida ali no impulso que calculamos.
Passo 2
Como os corpos tem velocidades com sentidos opostos inicialmente,elas também terão sinais opostos. A partir da conservação do momento linear no sistema, temos:
Agora que temos a velocidade final dos dois blocos (saem juntos), escolhemos um deles e calculamos a variação do momento linear.
Como a força que um bloco exerce no outro é igual à força recebida por ele, tanto faz qual dos blocos escolhemos.
Faremos para o primeiro:
Pronto, achamos a força . Como o gráfico trabalha com o módulo, o valor de será positivo. Arrumando a potência de , temos:
Resposta
Letra (C)