Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Aproximação Linear de uma Função de Várias Variáveis

Ver Teoria
Exercício 3012345678910111213141516171819202122232425262728293132333435363738394041

Enunciado

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, São Paulo: CENGAGE learning, 2010, pp. 855, exercício 23

(Cap 14.4 – Ex 23) Utilize a tabela do Exemplo 3 para encontrar a aproximação linear da função humidex quando a temperatura está próxima de 32 ° C e a umidade relativa do ar é de aproximadamente 65 % . Estime também o humidex quando a temperatura é de 33 ° C e a umidade relativa, 63 % .

Passo 1

Show de bola, galera! Vamos resolver essa questão em 3 passos!

Antes de começarmos a resolver a questão, vamos relembrar a tabela do enunciado:

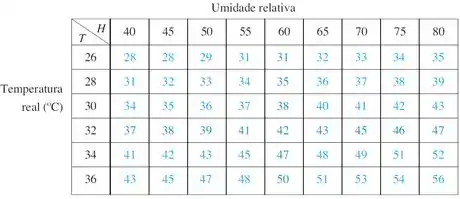
Nesse primeiro passo, vamos só relembrar os conceitos principais para resolver a questão, beleza?

Como estamos procurando uma aproximação para uma função de 2 variáveis, devemos nos lembrar que essa aproximação será dada por:

f x , y ≈ f a , b + f x a , b x - a + f y a , b y - b

Show? Lembrou? De boas, né....beleza.

Agora vamos relembrar o procedimento que a gente pode utilizar para calcular uma aproximação para derivada quando temos diversos valores de função apresentados igual aos que estão na tabela do enunciado.

Nesses casos, vamos fazer 2 estimas para f x ( a , b ) e f y ( a , b ) , respectivamente, e usar a média dessas estimativas como estimativa final. Ficou confuso?

Vamos fazer o seguinte:

f x , 1 a , b  estimativa 1 para  f x a , b

f x , 2 a , b  estimativa 2 para  f x a , b

f y , 1 a , b  estimativa 1 para  f y a , b

f y , 2 a , b  estimativa 2 para  f y a , b

f x a , b ≅ f x , 1 a , b + f x , 2 a , b 2

f y a , b ≅ f y , 1 a , b + f y , 2 a , b 2

Bom...melhor irmos logo fazer as contas, né

Passo 2

f x , 1 32,65 = f 34,65 ⏞ 48 - f 32,65 ⏞ 43 2 = 5 2

f x , 2 32,65 = f 30,65 ⏞ 40 - f 32,65 ⏞ 43 - 2 = 3 2

f y , 1 32,65 = f 32,70 ⏞ 45 - f 32,65 ⏞ 43 5 = 2 5

f y , 2 32,65 = f 32,60 ⏞ 42 - f 32,65 ⏞ 43 - 5 = 1 5

Assiiimm....

f x 32,65 ≅ f x , 1 32,65 + f x , 2 32,65 2 = 5 2 + 3 2 2 = 2

f y 32,65 ≅ f y , 1 32,65 + f y , 2 32,65 2 = 2 5 + 1 5 2 = 3 10

Passo 3

Looogooo, voltando para a aproximação...

f x , y ≈ f 32,65 + f x 32,65 x - 32 + f y 32,65 y - 65

f x , y ≈ 43 + 2 x - 32 + 3 10 y - 65

Para a aproximação que queremos no enunciado:

f 33,63 ≈ 43 + 2 33 - 32 + 3 10 63 - 65 = 44,4

Resposta

f x , y ≈ 43 + 2 x - 32 + 3 10 y - 65

f 33,63 ≈ 44,4

Exercícios de Livros Relacionados

O índice de sensação térmica W é a temperatura que se sente quando a temperatura real for T e a velocidade do vento, v ; portanto, podemos escrever W = f T , v . A tabela de valores a seguir foi extra
A altura h de ondas em mar aberto depende da velocidade do vento v e do tempo t durante o qual o vento se manteve naquela intensidade. Os valores da função h = f( v , t ) são apresentados na seguinte
Explique por que a função é diferenciável no ponto dado. A seguir, encontre a linearização L ( x ,y ) da função naquele ponto. f x ,y = 1 + y 1 + x ( 1 ,3 )
Utilize a tabela do Exemplo 3 para encontrar a aproximação linear da função humidex quando a temperatura está próxima de 94 °F e a umidade relativa do ar é de aproximadamente 80 % . Estime também o hu
Verifique a aproximação linear em 0,0 . 2 x + 3 4 y + 1 ≈ 3 + 2 x - 12 y