Considere a função
- Calcule e e explique as suas interpretações geométricas
- Encontre a taxa máxima de variação da função no ponto . Determine a direção em que essa taxa máxima de variação ocorre
- Encontre a equação do plano tangente ao gráfico de no ponto
- Encontre a linearização de em , use-a para calcular aproximadamente e explique por que é possível usar a sua linearização para aproximar .
Passo 1
Pra começar, vamos definir uma coisa importante. A questão pede e . O subscrito significa que é a primeira derivada em relação a e , respectivamente. Portanto, derivamos:
Em relação a primeiro, temos:
Usando a famosérrima regra da cadeia, temos:
Veja que até o momento, não derivamos nada em relação a meeesmo, o que nos leva a um pulo do gato enorme, que é a derivada em relação a , que vai ter a mesma cara já que até então tem os mesmos passos:
Derivando os dois, temos:
Calculando e , basta trocarmos por nas duas definições acima:
O que resulta em:
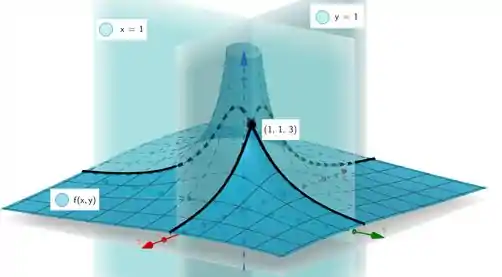
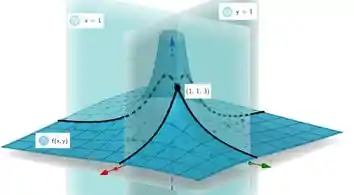
Qual a implicação geométrica disso? Bem galera, tradicionalmente, quando derivamos, achamos a inclinação de uma tangente! Aqui não será diferente! Teremos então que a curva de interseção de com o plano e com o plano , apesar de serem diferentes, terão uma reta tangente com a mesma inclinação em e de inclinação .
Passo 2
A letra vai pedir pra gente aplicar uma definição importantíssima: a de variação máxima. Galera, ela nada mais é do que o vetor gradiente:
No ponto , como o enunciado pede, não tem mistério, vamos ter:
Ok então. Sabemos a direção na qual a variação máxima acontece, mas e a taxa de variação máxima? Pra achar a taxa, fazemos o módulo desse vetor aí de cima:
Passo 3
Aqui também vai ser tranquilin, afinal equação de plano tangente tem uma fórmula geral bem bonita que ajuda a gente:
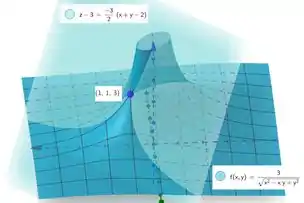
Onde é o ponto de tangência. Substituímos então e achamos:
E olha que bonito que fica no gráfico:

Passo 4
Hora de fechar com chave de ouro e fazer a última letra! Na verdade nem tem muito mistério. Afinal, o plano tangente é a própria linearização para uma superfície em determinado ponto. Como ainda estamos falando do mesmo ponto, podemos isolar na equação do plano tangente e obter:
Vamos ter que quanto está perto de . E taí! A questão não pediu no ponto ? Tudo o que precisamos fazer é calcular :
Resposta
Letra a)
- A curva de interseção de com o plano e com o plano , apesar de serem diferentes, terão uma reta tangente com a mesma inclinação em e de inclinação .
Letra b)
- Variação máxima ocorre na direção a uma taxa máxima de
Letra c)
Letra d)