Considere a função
a) Encontre o domínio e a imagem de .
b) Encontre a taxa máxima de variação da função no ponto . Determine a direção em que essa taxa máxima de variação ocorre.
c) Identifique e esboce a superfície de nível que passa pelo ponto . Esboce o vetor gradiente no mesmo ponto . Qual é a relação geométrica entre a superfície de nível e o vetor gradiente?
d) Encontre a linearização de em , use-a para calcular aproximadamente e explique por que é possível usar a sua linearização para aproximar .
Passo 1
a) Pensar em domínio de uma função é olhar para expressão dela e ver se tem denominador, raiz par ou log. Se tiver, a gente usa essas restrições aqui para criar inequações que descrevem nosso domínio:
E como a gente tem uma função de três variáveis, nosso domínio deve ser uma região no espaço tridimensional , tá? Vamos lá!
Mas olha para a nossa função
Ela não tem denominador, raiz ou log. Logo, ela não tem nenhuma restrição no domínio. Então nosso domínio é todos os reais no espaço :
Passo 2
Agora para olhar a imagem, a gente vai fazer algo parecido. Vamos olhar nossa função para ver se tem essas características:
A gente vê que a nossa função tem um exponencial. Aí a gente pode escrever:
Como o expoente desse pode assumir qualquer valor (já que não temos só termos positivos ou com raiz par), não temos outras características dessa função para avaliar a imagem.
Dessas coisinhas a gente tira que
Passo 3
b) Cara, guarda isso no seu coração:
A direção e o sentido de maior crescimento da função é a direção e sentido do vetor gradiente da função no ponto dado. Vamos calcular ele
Usando a regra da cadeia
Para as outras o cálculo é parecido:
Substituindo o ponto dado, que foi :
Então a direção e sentido da taxa máxima de variação é a direção e sentido de
Passo 4
Outra coisa para guardar no coração:
A taxa máxima de crescimento é o módulo do vetor gradiente, que vale:
Passo 5
c) Para achar a superfície de nível no ponto , a gente precisa substitui ele na nossa função
Aí a nossa superfície de nível vai ser a equação que a gente encontra quando iguala essa constante que a gente achou, o , com a expressão de . Assim oh:
Essa é a nossa superfície de nível! Como ela tem apenas dois termos ao quadrado, isolados e positivos. E do outro lado a gente só tem o , dizemos que isso é um paraboloide elíptico!
Uma outra forma de ver isso, que também vai ajudar no esboço, é achar a interseção dessa superfície com os planos . (seus traços) Vamos ter parábolas viradas para cima que passam pela origem. Daí que vem o nome paraboloide.
O esboço dele fica assim
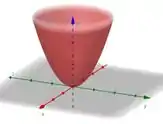
Percebe que ele passa pela origem, já que satisfaz sua equação.
Passo 6
Agora a gente faz o vetor gradiente no ponto , que é
Fica assim
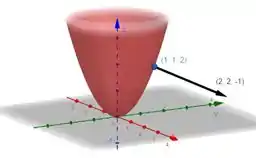
A relação geométrica entre esse vetor e a superfície é que esse vetor é normal a nossa superfície.
O vetor gradiente de uma função de 3 variáveis em um ponto é normal a superfície de nível que passa por esse ponto.
Passo 7
d) A fórmulinha da aproximação linear é:
Onde é o ponto que ele pediu a aproximação, ou seja
E a gente tem do vetor gradiente nesse ponto que
E vimos também que
Substituindo essas informações na fórmulinha
Passo 8
Agora a gente usa essa expressão para calcular a aproximação de
E a gente pode usar essa aproximação linear no ponto para calcular , porque os pontos e estão bem próximos, e as derivadas parciais de :
são contínuas no ponto
Resposta
a),
b) Taxa máxima ocorre na direção e sentido de . E vale .
c) 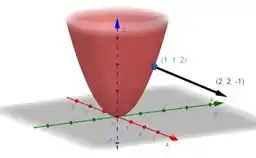
Temos um paraboloide elíptico e o vetor gradiente é normal a essa superfície.
d)
E a gente pode usar essa aproximação linear no ponto para calcular , porque os pontos e estão bem próximos, e as derivadas parciais de são contínuas no ponto