Um capacitor é composto de placas paralelas quadradas de lado e separadas por uma distância . Um bloco de material dielétrico, também de lado e espessura e de constante de permissividade é introduzido no capacitor, preenchendo completamente o espaço entre as placas.

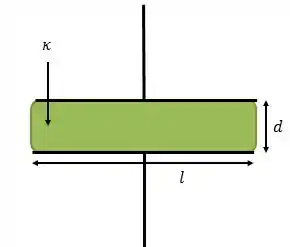
1. Escreva as expressões para as capacitâncias para a situação de vácuo entre as placas (sem o dielétrico) e quanto tem-se o dielétrico de constante de permissividade ;
2. Calcule a variação (devido à colocação do dielétrico) de energia armazenada no caso das placas, quando a carga, nas placas da armadura é mantida constante;
3. Calcule a mudança de energia armazenada (devido à colocação do dielétrico) quando a diferença de potencial entre as placas for mantida constante;
4. Por fim, a placa é parcialmente deslocada, deixando um comprimento do espaço livre, qual será a nova capacitância?

b) Calcule a variação (devido à colocação do dielétrico) de energia armazenada no caso das placas, quando a carga, nas placas da armadura é mantida constante;

É importante lembrar que, quando adicionamos o dielétrico ao capacitor, as únicas grandezas que variam são a capacitância e a diferença de potencial entre os terminais do capacitor. A menos que a questão diga algo sobre isso, a carga permanece constante.

Assim, para a situação inicial, a energia armazenada no capacitor é dada por:

E para quando temos o dielétrico entre as placas do capacitor:

Onde . Logo:

Portanto, a variação de energia será:

c) Calcule a mudança de energia armazenada (devido à colocação do dielétrico) quando a diferença de potencial entre as placas for mantida constante;

Opa! Então nesse caso, se a diferença de potencial permanece constante, isso significa que a carga no capacitor variará quando adicionarmos o dielétrico.

Se permanece constante, podemos reescrever a fómula para a energia armazenada no capacitor em função de .

Agora sim! Inicialmente, a energia armazenada no capacitor será:

E a energia armazenada no capacitor após adicionarmos o dielétrico será:

Portanto, a variação de energia será dada por:

d) Por fim, a placa é parcialmente deslocada, deixando um comprimento do espaço livre, qual será a nova capacitância?

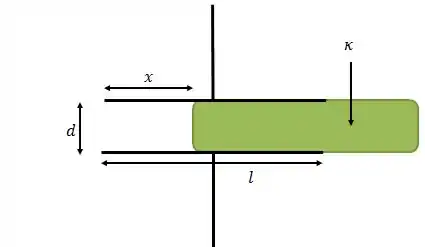
Quando o problema tem essa cara, podemos usar a situação de dois capacitores arrumados em paralelo.

O primeiro capacitor (esquerda) terá área e distância entre as placas de , tendo apenas vácuo no espaço entre as placas. O segundo capacitor (direita) terá área e distância entre as placas de , possuindo o dielétrico de constante no espaço entre as placas.

Sabendo que a capacitância para capacitores de placas planas e paralelas é dada por:

As capacitâncias para cada lado será:

Para capacitores em paralelo, a capacitância equivalente será: