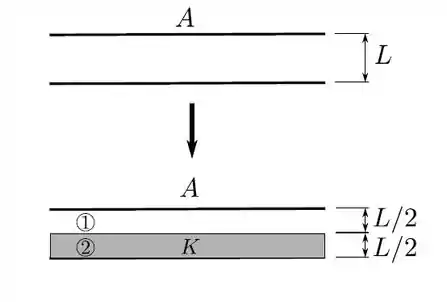
Um capacitor plano-paralelo tem placas idênticas de área , cada uma, com separação entre elas (conforme parte superior da figura ao lado). Numa primeira etapa, tal capacitor é ligado a uma bateria até atingir um módulo de diferença de potencial entre suas placas e, imediatamente, desconectado da bateria.

1. Determine o módulo do campo elétrico e a energia eletrostática armazenada

Numa segunda etapa um isolante de constante dielétrica é inserido no capacitor, preenchendo pela metade região entre suas placas, conforme mostrado na parte inferior da figura ao lado.

2. Determine o módulo da nova diferença de potencial entre as placas.
3. Determine o módulo (, , ) do novo campo elétrico em cada uma das duas “metades” ( e ) entre as placas.
4. Determine a nova energia eletrostática armazenada .

Agora podemos aplicar a fórmula da energia armazenada para matar a questão, escolhendo a mais adequada:

A capacitância podemos jogar direto aquela nossa fórmula de bolso:

Como temos duas regiões em série, a voltagem entre elas é a soma das voltagens. Logo:

Podemos achar esses módulos de voltagens integrando o campo, que é uniforme, na região onde estão definidas cada uma delas:

Já o outro, é a mesma integral só que o campo elétrico é dividido pela constante dielétrica:

Somando:

Substituindo o valor da voltagem original :

O campo na primeira região é o mesmo de antes, porque lá não mudou nada.

Na segunda região (onde enfiam um dielétrico) é só dividir pela constante dielétrica:

Para calcular a nova energia armazenada é só substituir na fórmula:

A voltagem nova nós temos... A capacitância nova não... Vamos ter que calcular ela ou tentar outra fórmula. Eu tentaria brincar com essa aqui:

A voltagem nós temos e a carga nova é igual. A carga de dois elementos em série é igual. Logo:

A carga antiga entra na equação relacionando com a capacitância antiga:

Voltando então

E a capacitância antiga nós temos.

E finalmente