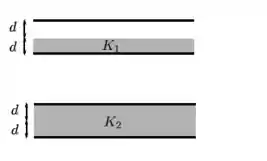
Um capacitor de placas planas e paralelas está parcialmente preenchido por um material isolante de constante dielétrica K1 = 3 que possui espessura d igual à metade da separação entre as placas (2d), como mostra a figura abaixo. Em seguida, com a diferença de potencial entre as placas mantida constante por uma bateria, o material isolante é substituído por um outro, que possui constante dielétrica K2 = 2 e que ocupa totalmente o espaço entre as placas. Qual é a razão U1/U2 entre as energias armazenadas pelo capacitor antes e depois da mudança do dielétrico?

(a) 3/4

(b) 4/3

(c) 4

(d) 1/4

(e) 2/3

(f) 3/2

(g) 1

Bom, sabemos que a energia armazenada em um capacitor é

Esse é a capacitância e é a tensão.

Na primeira situação, temos uma associação em série de dois capacitores. Então a capacitância equivalente é

A capacitância de um capacitor de placas paralelas é

O é a área da placa e o é a distância entre elas, o é a permissividade elétrica do meio. E

Substituindo isso tudo:

Então a energia nessa situação é:

Agora, vamos calcular o

E a capacitância para essa situação é:

Agora é porque é a nova distância entre as placas, ok?

Então fica:

Calculando a razão entre e :

Simplificando tudo: