- Um capacitor de placas paralelas com área de cada placa e separação entre elas , está imerso no vácuo. Calcule a capacitância deste capacitor.
- Uma placa de material dielétrico com constante dielétrica , espessura e área , é colocada no interior do capacitor, a meia distância de cada uma das placas do mesmo, de maneira que nenhuma fração do dielétrico fique fora do capacitor. Calcule a nova capacitância do capacitor.
Passo 1
Vamos dividir o nosso problema em dois instantes:
- Primeiro instante, temos um capacitor carregado sem o dielétrico (veja a OBS1):
- Segundo instante, temos um capacitor carregado com o dielétrico:
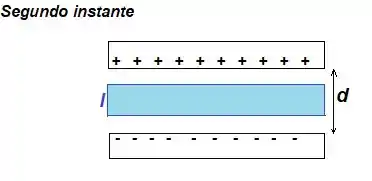
OBS1: Materiais dielétricos são materiais isolantes colocados entre uma placa e outra de um capacitor para evitar que as duas placas se encoste uma na outra. ;)
OBS2: AH! Embora a gente desenhasse o capacitor em duas dimensões, te em mente que isso está no 3D, já eh? O capacitor na verdade são duas chapas paralelepipédicas.
O item do problema acontece no primeiro instante e é no item da C, é que vamos considerar o dielétrico na brincadeira! Vamos nessa?
Passo 2
Cara, a capacitância de um capacitor (no vácuo e sem nenhum material isolante no meio) só depende das condições físicas do material:
Onde é a área da chapa do capacitor e a separação entre as placas. Como os valores de e de foram dados como constantes, podemos deixar assim!
Ta aí! A capacitância do nosso capacitor nesse primeiro momento.
Passo 3
Bem, com a capacitância em mãos também podemos determinar a quantidade de cargas livres que se juntaram no capacitor, pela relação...
Onde é o potencial inicialmente entre as placas. E o interessante é que com o dielétrico ou sem, a carga livre que se juntou na superfície do capacitor vai ser a mesma...
E é da junção dessas duas expressões que a gente vai tirar a relação da nova capacitância com a inserção do dielétrico...
Repare que precisamos então encontrar o valor do novo potencial que surge ao se inserir o dielétrico. E aí é só substituir e correr para o abraço. Vamos nessa?
Passo 4
Cara, para um capacitor sem nenhum dielétrico, o campo magnético que se estabelece entre as placas é ...
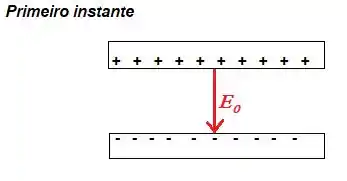
Uma constante que se relaciona com o potencial do capacitor por...
Mas esse só existe no vácuo. Porque quando você insere o dielétrico, onde o dielétrico está o campo se reduz para (Mas continua existindo onde não se tem vácuo):
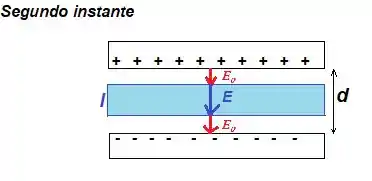
Mas o interessante é que se você conhecer a constante dielétrica do material (no caso é ) então você conhece o valor do campo elétrico pela relação...
Tá, mas e daí?
Passo 5
POW! Para encontrar a nova capacitância, precisamos encontrar primeiro qual é o novo potencial entre as placadas do capacitor e que vai ser igual a soma dos potenciais...
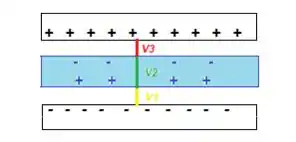
E para isso, precisamos somar os três potenciais:
O campo elétrico nessas três regiões embora ele mude de para dentro do material dielétrico, ele continua constante e sempre pra baixo. Desse modo podemos usar a definição de que...
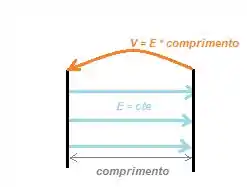
Então...
Repare que o único trecho onde o campo elétrico muda dentro da região que ele vale conforme calculado no último item...
Como o campo ...
E ainda, como ...
Passo 6
Bem, agora finalmente podemos determinar uma nova relação para a nova capacitância dado que para o capacitor ainda continua válida a expressão:
Como encontramos no início do problema...
Legal, neh?
Resposta
Ei, a resposta está no passo a passo :)