Um capacitor de placas planas e paralelas (área e separação ) é carregado até atingir uma diferença de potencial e uma carga . Uma placa dielétrica, de constante e espessura , é introduzida entre as placas do capacitor, conforme a figura.

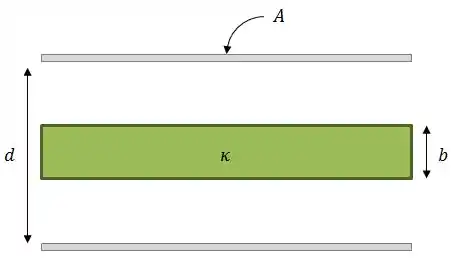
Encontre:

O campo elétrico no espaço vazio situado entre as placas do capacitor e a placa do dielétrico;

O campo elétrico dentro da placa dielétrica;

A diferença de potencial entre as placas do capacitor depois da introdução da placa dielétrica;

A capacidade do capacitor, depois da introdução da placa dielétrica, em função de , , e a permissividade ;

O campo elétrico dentro da placa dielétrica;

O campo elétrico no interior do dielétrico é dado por:

Onde é o campo elétrico na região sem o dielétrico. Portanto, substituindo pela expressão que encontramos na letra , teremos:

A diferença de potencial entre as placas do capacitor depois da introdução da placa dielétrica;

A diferença de potencial entre as placas de um capacitor está associada ao campo elétrico por:

Onde é a separação entre as placas.

Aqui, essa região pode ser dividida em três partes:

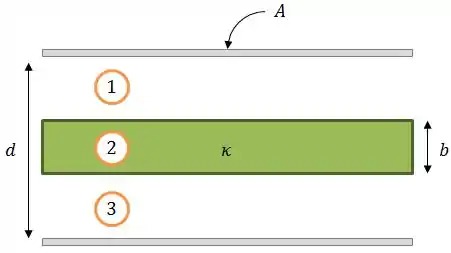
Eu sei que pode parecer bizarro olhando assim de cara, mas uma coisa que pode simplificar é se visualizarmos esse capacitor, na verdade, como uma associação de três capacitores em série: o primeiro sem dielétrico e separação ; o segundo com dielétrico e separação ; e o terceiro sem dielétrico e separação .

Assim, a diferença de potencial entre as placas será:

Sendo assim:

Agora é só organizar esse cara:

Finalmente:

A capacidade do capacitor, depois da introdução da placa dielétrica, em função de , , e a permissividade ;

Assim como falamos na letra , podemos imaginar esse cara como uma associação de 3 capacitores em série.

Sendo assim:

Como o primeiro e o terceiro são iguais, vamos dar uma simplificada nisso, falando que :

Onde:

Substituindo de volta na expressão de :

Agora é só dar uma arrumada nessa bagunça até ficar com uma cara decente:

Finalmente: