Um capacitor de placas planas e paralelas possui inicialmente vácuo entre suas placas, como mostrado na figura abaixo (painel à esquerda). Ele é carregado por uma bateria que fornece uma diferença de potencial constante entre as placas.
A seguir, mantendo a bateria conectada, insere-se no capacitor um material dielétrico de constante dielétrica e espessura igual à metade da distância entre as placas, como mostrado no painel direito da figura abaixo.
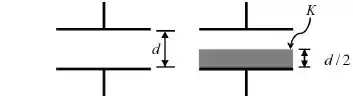
A razão entre as energias armazenadas pelo capacitor depois e antes da inserção do dielétrico vale:
.
.
.
.
.
.
Passo 1
A energia potencial armazenada no capacitor é dada por:
Onde, para um capacitor de placas paralelas no vácuo, a capacitância é dada por:
Em ambos os casos, o capacitor é alimentado por uma fonte que fornece uma diferença de potencial constante entre as placas. Então, tanto antes, quanto depois de inserir o dielétrico, a diferença de potencial entre as placas é .
Passo 2
Antes de colocar o dielétrico, a energia armazenada no capacitor é dada por:
Passo 3
Após inserir o dielétrico, é como se tivéssemos dois capacitores em série, cada um de largura . Logo:
Quando dois capacitores estão em série, a capacitância equivalente é dada por:
Substituindo as expressões de e , teremos:
Assim, a energia após a inserção do dielétrico será:
Passo 4
Finalmente:
Simplificando, teremos:
A resposta certa é a letra .
Resposta
.