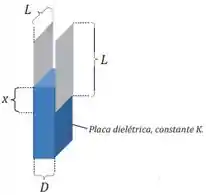
Duas placas condutoras quadradas, cada qual com lado igual a , são separadas por uma distância . Uma placa dielétrica com constante dielétrica e com dimensões é inserida até uma distância no espaço entre as placas, como indica a figura.
(a) Calcule a capacitância do sistema.
(b) Suponha que o capacitor seja conectado a uma bateria que mantém uma diferença de potencial constante entre as placas. Se a placa dielétrica for inserida até uma distância adicional no espaço entre as placas, mostre que a variação de energia acumulada é dada por:
(c) Suponha que, antes de a placa se mover uma distância , as placas sejam desconectadas da bateria, de modo que as cargas das placas permaneçam constantes. Determine o módulo da carga em cada placa e a seguir mostre que, quando a placa penetra mais uma distância no interior do espaço entre as placas, a energia acumulada varia de uma quantidade igual em módulo, mas de sinal contrário ao valor encontrado no item (b).
Passo 1
(a) Calcule a capacitância do sistema.
Vamos imaginar que o dispositivo da figura seja uma associação de dois capacitores em paralelo, sendo que um deles possui um dielétrico entre suas placas. As capacitâncias para os capacitores sem dielétrico e com dielétrico são dadas por:
Fazendo a associação em paralelos, vamos ter a seguinte capacitância equivalente:
Passo 2
(b) Suponha que o capacitor seja conectado a uma bateria que mantém uma diferença de potencial constante entre as placas. Se a placa dielétrica for inserida até uma distância adicional no espaço entre as placas, mostre que a variação de energia acumulada é dada por:
A energia acumulada no capacitor pode ser calculada como:
Podemos substituir na expressão acima o valor da capacitância equivalente que calculamos. Temos, então:
Podemos agora derivar em relação a para calcular a taxa de variação:
Por fim, temos que:
Passo 3
(c) Suponha que, antes de a placa se mover uma distância , as placas sejam desconectadas da bateria, de modo que as cargas das placas permaneçam constantes. Determine o módulo da carga em cada placa e a seguir mostre que, quando a placa penetra mais uma distância no interior do espaço entre as placas, a energia acumulada varia de uma quantidade igual em módulo, mas de sinal contrário ao valor encontrado no item (b).
A carga acumulada é dada por:
Substituindo o valor de na expressão acima, temos:
Já a energia acumulada é calculada como:
Bem, como queremos calcular a taxa de variação de em relação a , podemos derivar a expressão acima usando a regra da cadeia. Vamos lá:
onde consideramos que a carga é constante! Lembrnado que as placas agora estão desconectadas da bateria ;)
Vamos continuar, agora sim substituindo o valor de na expressão aí de cima:
que é onde queríamos chegar!
Resposta
(a)
(c)