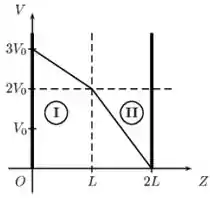
A figura abaixo mostra o gráfico do potencial elétrico no interior de um capacitor de placas condutoras planas e paralelas posicionadas em e. Considere que é muito menor que as dimensões das placas e que o sistema está em equilíbrio eletrostático. Sabendo que a região (II) está preenchida por vácuo, podemos afirmar que a região (I) está preenchida por um material isolante de constante dielétrica igual a:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Nessa questão nós vamos analisar o gráfico.
i) Olha só, entre e , o potencial cai de para , ou seja, cai em apenas uma unidade.
ii) Entre e , que é onde tem vácuo, o potencial cai de para , ou seja, cai em duas unidades, o dobro da queda em i). Logo, a nossa constante dielétrica, que é inversamente proporcional ao potencial, tem valor .
Portanto, a alternativa correta é a letra A.
Resposta
(a)