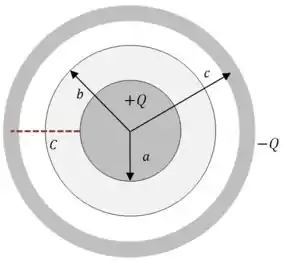
Uma esfera condutora de raio , carregada com carga , está cercada por uma camada condutora esférica concêntrica de raio , carregada com carga . O espaço entre e está preenchido com um material dielétrico de constante dielétrica . O espaço entre e é vácuo. Determine:

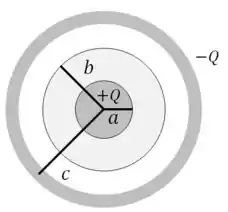
a) O vetor campo elétrico para:

i.

ii.

iii.

b) A diferença de potencial entre e , ou seja .

c) A capacitância do conjunto.

Pra encontrar o campo elétrico na região com , vamos escolher uma esfera como nossa superfície gaussiana, e uma que tenha um raio exatamente nesse intervalo:

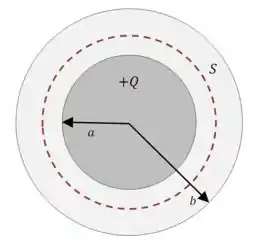
Por simetria esférica, o campo deve apontar na direção radial, que nós vamos chamar de :

E o vetor , que deve ser normal à nossa superfície Gaussiana, também aponta nessa mesma direção:

Então, como , aquele produto interno dentro da integral fica:

Ou seja:

O campo elétrico é constante ao longo da superfície, então podemos tirar ele da integral:

Agora essa integral dupla de é simplesmente a área da nossa superfície gaussiana, que é uma esfera de raio :

Então, como a carga contida no interior da superfície é mesmo:

Agora é só isolar o campo elétrico nessa equação:

E como vimos antes:

Então:

Na região .

O que acontece na região ? Agora estamos fora do dielétrico e ainda dentro da casca esférica de raio .

Bom, é só dar uma esticada naquela nossa superfície gaussiana:

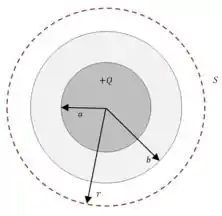
Bom, a quantidade total de carga contida na nossa gaussiana continua a mesma, concorda? Então o que tem de errado em continuar usando a nossa fórmula de antes?

Ah! Uma diferença importante, agora a nossa gaussiana não está no interior do dielétrico, então temos que usar (que é o valor da constante dielétrica no vácuo).

Então essa é a fórmula do campo elétrico na região .

E agora vamos ver como fica a situação quando partimos para a região :

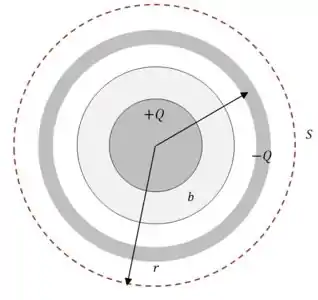
A simetria continua a mesma, então aquela integral de antes continua igual (ainda com ):

Mas agora a carga total contida na gaussiana é zero:

Então:

Ou seja:

Na região .

(b) O próximo passo é calcular a diferença de potencial entre as duas partes carregadas.

Aquele dielétrico ali pode te confundir um pouco, mas vamos com calma.

A definição do potencial elétrico continua valendo! Vamos usar ela aqui:

O que essa integral aí está dizendo? Bom, a gente tem que escolher um caminho que vá desde a camada de raio até a superfície da esfera de raio . Que tal uma linha reta?

O campo elétrico é paralelo àquele caminho em todos os pontos da trajetória, então o produto interno é:

E a integral é:

Mas o campo não é o mesmo o tempo todo! Entre e , a fórmula do campo é:

E entre e a constante vira , porque estamos no vácuo:

Quando colocamos isso na integral acontece o seguinte:

Como a gente está indo do raio até o raio (ou seja, raio diminuindo):

Então, reorganizando um pouco:

A integral de é , então:

Agora vamos organizar um pouco:

Então essa é a diferença de potencial entre as duas superfícies!

(c) Agora a última etapa é calcular a capacitância do conjunto. Temos que usar essa fórmula aqui:

E é o módulo da carga em cada uma das placas, que no nosso caso é . Substituindo com a fórmula que a gente encontrou para o potencial entre as placas:

Dividindo os dois lados por e isolando :