Considere um capacitor esférico formado por um condutor interno de raio e um condutor externo de raio , conforme a figura. O espaço entre os condutores é preenchido com material de constante dielétrica .
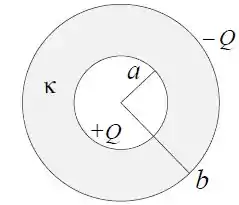
Carrega-se o condutor interno com carga e o externo com carga (cargas livres). O campo elétrico devido apenas a essas cargas livres é
Onde é a distância ao centro do capacitor esférico.
Escreva a expressão do vetor campo elétrico dentro do dielétrico .
Calcule a energia armazenada no capacitor na ausência de dielétrico (em função de , e ), e a energia na presença do dielétrico (em função de e ).
Calcule o vetor campo elétrico devido somente às cargas induzidas (ligadas) no dielétrico.
Passo 1
Escreva a expressão do vetor campo elétrico dentro do dielétrico .
O próprio problema já nos disse que o campo elétrico devido apenas às cargas livres é dado por
Quando colocarmos o dielétrico, a única diferença é que, agora, o campo elétrico será dado por:
Portanto:
Passo 2
Calcule a energia armazenada no capacitor na ausência de dielétrico (em função de , e ), e a energia na presença do dielétrico (em função de e ).
Beleza! Por definição, a energia armazenada em um capacitor é dada por:
Então, o nosso primeiro trabalho aqui é calcular .
Por definição, será dado por:
Onde .
Passo 3
Assim, a energia potencial é dada por:
Finalmente:
Passo 4
Quando adicionarmos o dielétrico, o potencial passará a ser:
Portanto:
Finalmente:
Passo 5
Calcule o vetor campo elétrico devido somente às cargas induzidas (ligadas) no dielétrico.
Nós falamos na letra que o campo elétrico com o dielétrico passa a ser
Na verdade, essa mudança ocorre devido ao campo elétrico das cargas induzidas que aparece por conta do material dielétrico.
Resumindo, o que acontece é o seguinte:
Portanto:
Resposta