Considere um capacitor de placas planas, paralelas, com área , separadas por uma distância no vácuo.
Calcule a capacitância deste capacitor no vácuo em função de ,
e .
Calcule a nova capacitância do capacitor se preenchermos parcialmente o espaço entre as placas com um material de constante dielétrica e espessura , conforme a figura. Forneça sua resposta em função de e .
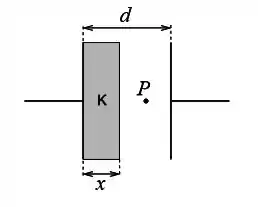
Calcule a densidade de energia num ponto da região sem dielétrico após ligarmos as placas do capacitor a uma bateria com uma diferença de potencial igual a . Forneça sua resposta em função de e
Passo 1
Talvez, você já saiba decorado essa resposta, que a capacitância de um capacitor é dada por:
Pois vimos isso na teoria, vimos ainda que a capacitância depende exclusivamente da geometria e componentes do capacitor.
Bem, mas como chegamos nessa fórmula, dado apenas a seguinte fórmula, dada no formulário:
Quando estudamos potencial, vimos que
Vishh, agora precisamos saber a fórmula do campo elétrico gerado por placas paralelas.
Bem, usando a lei de Gauss, como auxilio, e como uma placa paralela vai gerar um campo constante e sempre na direção perpendicular a sua superfície.
Vamos escolher como superfície gaussiana, um cubo fechado de lados iguais ao da placa do capacitor, assim a carga interna será a carga total da placa e só haverá fluxo de campo elétrico nas tampas do cubo, analisando apenas a tampa que está entre as placas do capacitor, teremos que
Como a área da tampa é
Assim, encontramos o valor do campo elétrico entre as placas do capacitor
Substituindo na equação do potencial temos que
Então, substituindo na equação da capacitância, temos
Boa!, chegamos no resultado que esperávamos.
Passo 2
Quando adicionamos um dielétrico entre as placas do capacitor vamos mudar o campo e o potencial entre as placas, certo?
Bem nesse caso, vamos ter duas regiões,
A região com o dielétrico e a região sem o dielétrico
Como o potencial depende da distância, teremos um potenciais diferente para as regiões (
Adotamos como nosso referencial o potencial na placa em que foi colocado o dielétrico, assim o potencial na região do dielétrico é
obs: estamos calculando o potencial na região do dielétrico, porém antes de ser posto o dielétrico, por isso podemos dizer que o campo é .
Assim, temos que
Como descobrimos o valor do novo potencial, podemos escrever a equação da capacitância
Boa, no item já vimos que
Disso, tiramos que
Voltando a equação da capacitância temos que
Passo 3
A equação da densidade de energia em um dado ponto é
O campo elétrico, você teve que calcular lá no item ,
Então, podemos reescrever a equação da densidade de energia, da seguinte forma:
Ainda falta relacionarmos o a carga com a capacitância, mas isso é moleza para gente, só lembrarmos da primeira fórmula que usamos
O potencial foi dado, e terminamos de descobrir no item
Então,
Por isso, a densidade de energia é
Chegamos, na densidade de energia em função e