Seja o capacitor cilíndrico da figura abaixo, com a placa interna carregada com carga negativa , de tal forma que a placa externa tenha a mesma carga, em módulo, porém positiva.
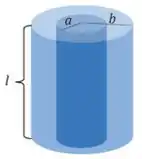
(a) Determine a densidade de energia entre suas placas.
(b) Determine a energia armazenada neste capacitor, usando a relação , onde é um elemento de volume.
Passo 1
(a) Determine a densidade de energia entre suas placas.
Percebemos, inicialmente, que p campo elétrico está orientado de fora para dentro. Podemos usar a lei de Gauss para determinar o módulo do campo elétrico na região entre as placas. Aqui vamos usar uma superfície gaussiana cilíndrica de raio :
Passo 2
A densidade de energia será dada por:
Substituindo o valor de encontrado no Passo 1, temos que:
Passo 3
(b) Determine a energia armazenada neste capacitor, usando a relação , onde é um elemento de volume.
A energia armazenada será:
em que . Assim sendo, utilizando a expressão para na equação acima, ficamos com:
Resposta
(a)
(b)