Um capacitor é constituído de cilindro com raio e carga coaxial com uma casca cilíndrica fina de raio e carga . O cilindro e a casca cilíndrica têm ambos altura , conforme a figura .
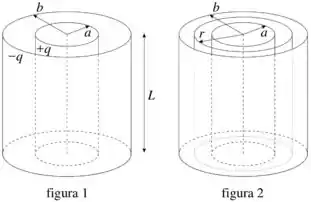
(a) Calcule o vetor campo elétrico dentro do capacitor, na região . Despreze efeitos de borda.
(b) Calcule a capacitância do capacitor.
(c) Calcule a energia contida no interior de um cilindro de raio () e altura , coaxial com o capacitor, conforme a figura .
Passo 1
Aqui queremos calcular o campo elétrico entre as duas cascas cilíndricas na figura .
Como o enunciado diz para desprezarmos os efeitos de borda, isso equivale a dizer que o comprimento do cilindro é muito maior que os raios e .
Sabemos que o campo elétrico tem que apontar da placa com carga positiva para a placa com carga negativa. Como as duas placas são cilíndricas, o campo elétrico irá apontar na direção radial, ou seja, .
Passo 2
Agora podemos usar a lei de Gauss. A superfície gaussiana que iremos usar será um cilindro de raio () e altura .
O fluxo do campo elétrico através das tampas da nossa superfície será , já que os vetores unitários de área nas tampas estão na direção e o campo está na direção (ou seja, o campo é paralelo a essas superfícies).
Já o fluxo na parte lateral do nosso cilindro será tranquilo de calcular, pois o unitário de área agora é paralelo ao campo elétrico (na direção ).
Assim
Onde é a área lateral do nosso cilindro.
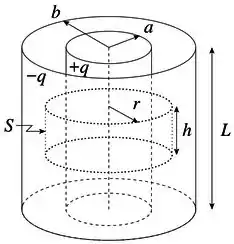
Pela lei de Gauss temos que a integral acima é a carga total dentro da nossa superfície gaussiana. Como para o cilindro de altura temos uma carga , para o cilindro de altura teremos um total de carga de
Agora podemos aplicar a lei de Gauss
Passo 3
Para calcular a capacitância precisamos lembrar que a capacitância é dada por
onde é a diferença de voltagem entre as placas.
Como já obtivemos o campo entre as placas, para achar a diferença de potencial, basta usar
A diferença de potencial é uma integral de caminho. Como queremos a diferença de potencial entre as duas placas, a integral de caminho partirá da placa interna e chegará à placa externa.
O melhor caminho será na direção radial ligando as duas placas. Dessa forma o nosso caminho será paralelo ao campo elétrico e terá mesma direção (apontando de dentro para fora) e o produto escalar dentro da integral será o produto das quantidades e .
Essa integralzinha será
Tudo bem aqui ter dado negativo já que a diferença que acabamos de calcular foi , ou seja, a diferença entre a placa negativa e a positiva. Para o cálculo da capacitância usaremos o módulo dessa quantidade
Assim
Repare que a capacitância só depende de seus aspectos geométricos como tem que ser! :)
Passo 4
Temos que a densidade volumétrica de energia do campo elétrico é
Para calcular a energia total do campo, temos que integrar essa quantidade no volume do cilindro de raio () e altura .
Como no interior do cilindro de raio não há campo elétrico, temos que integrar na coordenada radial de , até .
O elemento de volume será (coordenadas cilíndricas)