Um capacitor de placas planas e paralelas de área e separação preenchido, em uma metade, com um isolante de constante dielétrica , conforme mostra a figura abaixo. Nessa situação, a diferença de potencial entre as placas vale . Considere que é muito menor que as dimensões das placas e que o sistema se encontra em equilíbrio eletrostático.
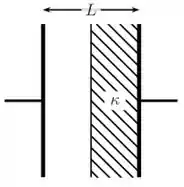
(a) Determine a capacitância do sistema.
(b) Determine a intensidade do campo elétrico no interior do capacitor nas regiões com e sem o isolante.
Passo 1
a) Pra calcularmos a capacitância vamos fazer o seguinte: e se a gente dividir o capacitor da figura em 2 capacitores? Um deles preenchido apenas por vácuo – com capacitância – e o outro preenchido pelo dielétrico – com capacitância .
Nós podemos fazer isso porque, perceba, a tensão entre as placas é a soma de (sem isolante) com (com isolante) e esses são proporcionais à carga armazenada nas placas, pois . Assim, dá pra gente perceber que e armazenam cargas iguais.
Vamos calcular a capacitância através da fórmula
Masss, temos que lembrar que o vale para ambas as placas.
Depois vamos associar e (que estão em série) para encontrarmos :)
Passo 2
Então vamos lá, calculando
Agora vamos calcular , lembrando que ele possui um isolante de constante dielétrica
Fazendo a associação em série de e :
Passo 3
b) A carga em um capacitor é dada por
Então, no nosso caso ela vai ser
Como o enunciado nos disse que é muito menor que as dimensões das placas, vamos tratar as placas como infinitas e uniformemente carregadas ok?
Aplicando a Lei de Gauss, sabemos que o campo elétrico na região preenchida por vácuo () vai ser
O campo elétrico na região com isolante vai ser
Resposta
- (sem isolante)
(com isolante)