Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fasores e Circuitos RLC

Ver Teoria
Exercício 106123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Letra (a). Num circuito LC, a energia num indutor é dada por:

E I N D = 1 2 . L . i 2

Essa energia é máxima quando a corrente é máxima. Isso ocorre quando toda a energia do circuito se concentra no indutor. Assim:

0,45   m J = 1 2 . 10,0   m H . I M A X 2 → I M A X = 0,3 A

Passo 2

Letra (b). Com as mudanças propostas, o circuito deixou de ser um L C simples e passou a ser um circuito R L C . Vamos então calcular a reatância de cada componente:

X C = 1 ω . C = 1 5000.10.10 - 6 = 20 Ω

X L = ω . L = 5000.10.10 - 3 = 50 Ω

X C I R C U I T O = R 2 + ω . L - 1 ω . C 2 = 4 0 2 + 50 - 20 2 = 50 Ω

A amplitude relativa pode ser calculada usando X L :

I M A X = 120 V X L = 120 V 50 = 2,4 A

Já o ângulo relativo entre a corrente e a fonte de tensão pode ser visto com maior facilidade quando a gente pensa no diagrama de fasores:

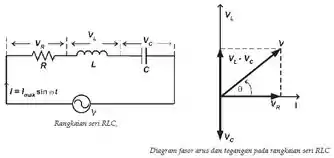
Veja só, sabemos que a tangente dessa diferença de fase vale:

tan ⁡ ϕ = V L - V C V R = X L - X C R = 50 - 20 40 = 0,75 = 3 4

Passo 3

Letra (c). Esse tipo de questão é rápido: é só comparar X L com X C e, por aqui, temos:

X L > X C → C o m p o r t a m e n t o   i n d u t i v o

Passo 4

Letra (d). A ressonância acontece quando X L se iguala a X C . Isso acontece quando:

1 ω . C = ω . L → ω 2 = 1 L . C → ω = 1 L C = 1 10 μ F . 10 m H = 1 10 - 5 . 10 - 2 ≈ 3,162   K H z  

Resposta

Letra (a)

I M A X = 0,3 A

Letra (b)

I M A X = 120 V X L = 120 V 50 = 2,4 A

tan ⁡ ϕ = V L - V C V R = X L - X C R = 50 - 20 40 = 0,75 = 3 4

Letra (c)

X L > X C → C o m p o r t a m e n t o   i n d u t i v o

Letra (d)

3,162   K H z  

Exercícios de Livros Relacionados

Na Fig. 31-37, um gerador trifásico G produz energia elétrica que é transmitida através de três fios. Os potenciais dos três fios (em relação a uma referência comum) são V 1 = As e nω t para o fio 1,
Que corrente contínua produz a mesma energia térmica, em um certo resistor, que uma corrente alternada com um valor máximo de 2,60A ?
A figura 31-35 mostra um gerador de CA ligado aos terminais de uma “caixa-preta”. A caixa contém um circuito R L C , possivelmente com mais de uma malha, cujos elementos e ligações são desconhecidos.
Um dimmer típico, com os que são usados para regular a luminosidade das lâmpadas do palco nos teatros, é composto por um indutor variável L (cuja indutância pode ser ajustada entre zero e L m a x ) li
Um gerador de CA alimenta uam carga resistiva em uma fábrica distante através de uma linha de transmissão de dois cabos. Na fábrica, um transformador abaixador de tensão reduz a tensão do valor de tra