No circuito de corrente alternada abaixo sabe-se que o valor quadrático médio da diferença de potencial . Além disso, sabe-se que a amplitude da d.d.p entre os pontos e é dada por: .

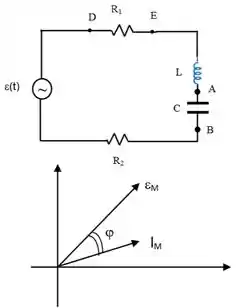
São conhecidos também os valores dos seguintes componentes:

Considerando o diagrama de fasores do circuito e sabendo que escreva a expressão de .

Determine o valor da capacitância .

Determine o valor do resistor .

Pelo gráfico dos fasores o circuito não está em ressonância. Para que isso aconteça é preciso aumentar ou diminuir o valor de ? Justifique as suas afirmações.

Uma vez estabelecida a ressonância no circuito, qual serão os novos valores das amplitudes de e ?

Precisamos determinar o valor da capacitância, para isso, iremos usar as seguintes relações:

Substituindo na segunda equação, temos:

Nós sabemos o valor máximo de , precisamos determinar , para isso, vamos usar a informação dada no enunciado, temos que , ou seja:

A corrente máxima será:

Agora é só substituir todos os valores na seguinte equação e correr pro abraço!

Para determinar a resistência , precisamos lembrar que está sempre em fase com a corrente , portanto, a componente da tensão total é a indicada na fórmula abaixo:

Além disso, sabemos que, como os resistores estão em série, temos:

Substituindo na primeira equação, temos:

Substituindo os valores, temos:

Para um circuito RLC, temos que a ressonância ocorre quando:

Vamos determinar ambas as reatâncias para avaliar a situação:

Reatância capacitiva:

Reatância Indutiva:

Temos então que , portanto o circuito apresenta comportamento capacitivo, para que as reatâncias se igualem, é preciso que o valor de aumente, podemos ver isso olhando para as definições das reatâncias, é diretamente proporcional à , enquanto é inversamente proporcional à .

Para determinar os novos valores de e para a nova situação, precisamos primeiro determinar o novo valor máximo de corrente:

Para :

Para :

Onde é:

Substituindo: