- Seja a função definida pelo gráfico
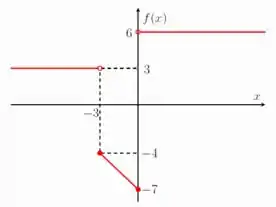

O valor de é
- ;
- ;
- ;
- .
Passo 1
Fala aí pessoal! Esse problema tá pedindo para que a gente olhe esse gráfico de aqui
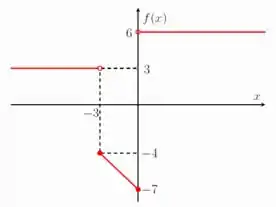
E encontre o valor de . Bom, olhando o gráfico a gente consegue já obter alguns valores mas aquele que é uma doideira não? Aquilo ali é uma função composta... o que a gente vai ter que fazer é ver o valor de primeiro e depois substituir esse resultado dentro de e ver no gráfico qual o resultado. Vamos lá resolver isso!
Passo 2
Bom, a gente tem que achar . Vamos começar com esse aí que é mais direto. Se olharmos no gráfico, temos que a função é pintada em no valor . Então temos:
Passo 3
Falta agora aquele primeiro termo ali. Vamos fazer ele por partes, primeiro a gente vê no gráfico quem é .
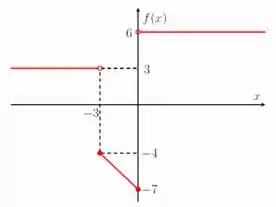
Não tem né? Mas a gente sabe que esse valor está na esquerda de e a função é uma reta que passa em nessa parte do gráfico... Ou seja:
Agora a gente pode substituir isso na nossa expressão:
Passo 4
Agora a nossa expressão ficou mais simples né? Precisamos, por fim, encontrar quem é . Olhando no gráfico a gente vê que a função para valores maiores que é uma reta que passa no . Então
E a nossa expressão fica:
E resolvemos esse problema 😊 Vamos para a próxima?
Resposta
Letra e.