Resolva a equação do primeiro grau:
Passo 1
Vamos lá!! Nesse exercício queremos encontrar o valor de que satisfaça a equação
Certo?
Para encontrarmos o valor de vamos isolar ele de um lado da equação. Assim, o resultado ficará do outro lado da igualdade!!
Passo 2
Por onde começamo então? Se você reparar, temos um e um dentro de um parêntesis, certo?
![]()
Vamos tentar sumir com eles para facilitar nossa vida. Para isso, vamos fazer a multiplicação distributiva. Repare que no termo é como se tivéssemos um multiplicando:
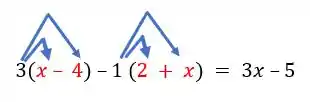
Fazendo a multiplicação, ficamos com
![]()
Podemos dar uma arrumada fazendo as multiplicações do lado esquerdo da equação
![]()
Beleza?!
Agora vamos somar todos os termos que tem o e todos os que não tem em ambos os lados da equação
![]()
Assim, ficamos com
![]()
Show de bola?!
Passo 3
Próximo passo vai ser isolar o que tem de um lado da equação e o que não tem do outro lado!!
Para isso, vamos somar ambos os lados da equação por
![]()
Somando novamente tudo o que não tem em ambos os lados da equação, ficamos com
![]()
Uma outra forma de ver isso é que quando passamos os números de um lado da igualdade pro outro, invertemos a operação. Aqui poderíamos pegar o e passar pro outro lado invertendo o sinal: como é negativo, passamos pro outro lado com o sinal de menos “+“ na frente!
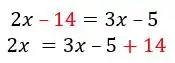
Podemos agora somar os termos que não tem do lado direito da equação, e assim ficamos com
![]()
Passo 4
Passo 5
Continuando o nosso objetivo de isolar o , iremos passar o termo do lado direito da equação para o lado esquerdo. Assim ficaremos com todos os termos que tem do lado esquerdo e os termos que não tem do lado direito da equação!!

Como o é positivo, ao passar pro outro lado ele ficará com o sinal negativo!
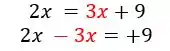
Agora é só fazer a continha do lado esquerdo
![]()
Pra finalizaaaaar, multiplicar ambos os lados da equação por , assim conseguimos sumir com o sinal negativo do lado esquerdo da equação:
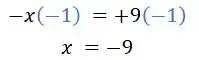
E assim encontramos o nosso valor de !!
Show de bola?!
Passo 6
Podemos confirmar que o valor que encontramos para está correto. Para isso, basta substituirmos na equação do enunciado o valor que encontramos.
Nossa equação do enunciado é
![]()
Substituindo o valor nessa equação
![]()
Fazendo as continhas em ambos os lados da equação, temos
![]()
Opa!!! Se você reparar temos essa igualdade e verdadeira, pois é igual a !! Então o valor de que encontramos está correto!!
