Considere o circuito de corrente alternada da figura 1, onde a frequência angular da fonte é. A posição relativa dos fasores da fonte e da corrente é mostrada na figura 2. Com a adição de um indutor em série , a posição relativa dos fasores muda para a da figura 3.
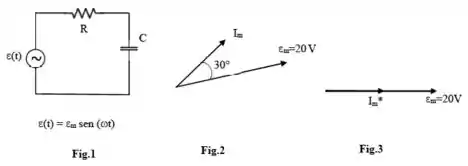
Determine, justificando todas as respostas:
- O valor da capacitância .
- A amplitude da corrente na ausência da indutância .
- O valor da resistência .
- A potência média fornecida pela fonte sem a indutância
- A potência média fornecida pela fonte com a indutância .
- A potência média absorvida pelo resistor sem e com a indutância .
Passo 1
a) Na figura 3, após a introdução do indutor no circuito, temos a corrente em fase com fonte alternada . Para resolver este item, vamos precisar nos lembrar que a fase entre a amplitude da corrente e amplitude da tensão da fonte é dada por
com , e sendo as amplitudes das voltagens em cada um dos elementos do circuito RLC em série.
Como a corrente está em fase com a ddp, então , o que nos dá, quando jogamos esse valor na expressão acima,
que é a condição de ressonância, ou seja, a condição que nos dá o maior valor para a amplitude da corrente e, nesse caso, a impedância é igual a resistência: .
De , tiramos que a capacitância é dada por
Passo 2
b) Sabemos que a amplitude da voltagem no capacitor é dada por
Ainda não temos o valor de . Para encontrar seu valor, vamos representar a figura 2 da seguinte maneira, em que colocamos a amplitude da voltagem e também a amplitude da voltagem no capacitor .
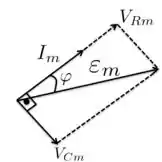
A gente vê que está em fase com a amplitude da corrente e que está atrasado de de em relação a . Como , a partir do triângulo acima, podemos tirar a seguinte relação
Substituindo em , temos
Passo 3
c) Ainda olhando para o triângulo acima, podemos também tirar a relação
Mas, como , temos
Passo 4
d) A potência média é dada por
em que , e é o fator de potência. Sem o indutor, teremos um valor médio igual a
Passo 5
e) Com o indutor, como mostra a figura 3, ocorre a ressonância, em que a corrente está em fase com a ddp alternada . Já vimos que nesse caso, e, então, o fator de potência será
Isso nos dá que a potência média será
Precisamos encontrar , precisamos nos lembrar que, na ressonância (), e a amplitude máxima da corrente será
Como isso, encontramos que a potência média será
Passo 6
f) Sem o indutor, temos uma potência média no resistor de
Com o indutor
Resposta
- Sem o indutor: Com o indutor: