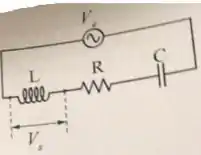
A figura mostra um filtro passa-alta, composto de um resistor de resistência , um indutor de indutância e um capacitor de capacitância , que permite a passagem de frequências altas com facilidade, porém atenua (ou reduz) a amplitude das frequências abaixo de uma frequência de corte. A amplitude da tensão de entrada é e a amplitude da tensão de saída é , que é medida nos extremos do indutor. Calcule, em função da frequência angular da fonte:
a) A amplitude da corrente que circula no circuito.
b) A amplitude da tensão de saída .
c) A relação entre as amplitudes, ou seja, .
d) Calcule o limite da razão para .
Passo 1
Esse é um problema clássico de circuito RLC. Vamos considerar a fonte senoidal e trabalhar com a notação complexa:
Como o circuito está em série, a impedância total do circuito é a soma das impedâncias de cada elemento:
Mas como , e , temos que
Lembre-se que e . Usando a lei de Ohm:
Cuidado para não confundir com . O primeiro é a corrente complexa e o segundo é a raiz quadrada de (unidade imaginária).
Com isso, podemos escrever:
Logo,
Para escrever isso de um jeito mais amigável, vamos multiplicar o numerador e o denominador por :
Além disso, podemos escrever
onde
Com isso, temos que
Portanto, a amplitude da corrente será
Substituindo as expressões de e :
No fundo, toda essa conta que eu fiz aqui é a teoria sobre circuitos RLC. Nos resumos do RespondeAí isso é explicado com mais detalhe, vai dar uma olhadinha lá se ficou alguma dúvida.
Passo 2
Para achar a tensão de saída no indutor, usamos:
Além disso,
Assim,
A amplitude dessa tensão complexa é simplesmente
Portanto,
Como :
Passo 3
Com a resposta do item (b) o item (c) é coisa mais fácil do mundo:
Vale ressaltar que a tensão no indutor está defasada com relação a tensão da fonte, e essa defasagem é dada por , onde foi achado no passo 1.
Por fim, no item (d), queremos calcular o limite . Para fazer esse limite, vamos olhar para o denominador primeiro:
Assim,
Tomando o limite com , temos que
Com isso,
Isso significa que para frequência altas, praticamente toda tensão de entrada “sai” no indutor. Daí o nome filtro “passa-alta”.
Aqui fechamos o problema 😉.