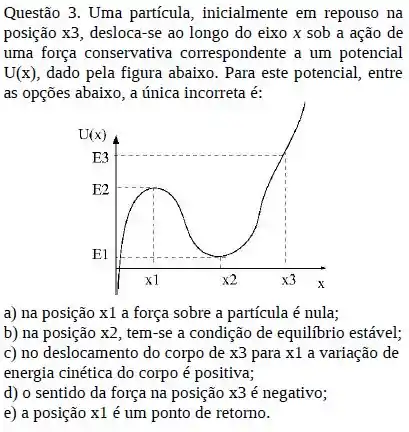
Passo 1
Letra a)
A força é nula sim! Como no gráfico de potencial é um ponto de inflexão, temos que a derivada desse ponto é , logo a força é nula!
Passo 2
Letra b)
O equilíbrio é estável, e só lembrar daquele lance da montanha russa se lembra? É um ponto de equilíbrio porque a derivada é zero nesse ponto.
Passo 3
Letra c)
Verdadeira também, como ele perde energia potencial, essa energia é convertida pra energia cinética !
Passo 4
Letra d)
Verdadeiro também, tipo, a força é o negativo da derivada da energia potencial.
Como a derivada é positiva, a força vai ser negativa !
Passo 5
Letra e)
Se todas as outras são verdadeiras ... essa aqui é falsa! Esse ponto não é um ponto de retorno, é um ponto de equilíbrio instável !
Obs: se você ficar com dúvida como eu sei o sinal das derivadas, cara, tem que ficar ligado na curva! Derivada é tipo o sentido que a curva ta indo, se ela ta crescendo a derivada é positiva, se ela ta descendo é negativa, se ela é tipo um ponto de inflexão a derivada é zero
Resposta
Letra e)