Se investigarmos o movimento dos átomos de uma molécula diatômica como o , veremos que eles executam um movimento vibracional. Porém, esse movimento não acontece para qualquer valor da energia mecânica, , dos átomos já que é possível dissociar a molécula. Levando em conta essas informações, podemos dizer que o movimento desses átomos pode ser descrito muito bem por uma energia potencial (sendo distância relativa entre os átomos), onde para e para , como a mostrada na figura abaixo.
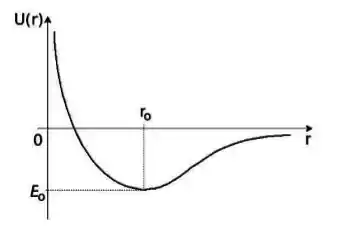
Considerando a energia potencial, podemos dizer que a força entre os átomos da molécula de é
Negativa quando e positiva para .
Positiva para e negativa quando .
Negativa para e positiva para .
Positiva sempre que .
Negativa sempre que .
Passo 1
Vimos que a força é menos a derivada da energia potencial.
Pelo gráfico temos que a derivada quando é positiva, pois é crescente e por isso a força é negativa.
Já quando o gráfico é decrescente e assim a derivada é negativa, e a força então é positiva.
Resposta
Alternativa