Uma partícula se desloca sobre o eixo sob ação de uma força resultante conservativa, cuja energia potencial está representada no gráfico a seguir. No instante inicial a partícula está no ponto . Considere duas situações distintas: na primeira ela possui energia mecânica e na segunda energia mecânica e sua velocidade inicial é no sentido positivo do eixo .
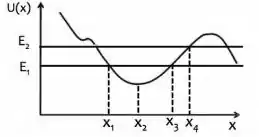
Comparando sempre as situações em que a energia mecânica é ou , qual das seguintes frases a seguir é verdadeira?
(a) Quando a partícula está na posição a força sobre ela é a mesma nos dois casos.
(b) Quando a partícula está na posição a sua velocidade é a mesma nos dois casos.
(c) Em ambos os casos, a posição é um ponto de retorno.
(d) Na posição a força sobre a partícula é nula apenas no caso em que a energia mecânica é .
(e) A posição é uma posição em que a energia cinética é máxima, no caso em que a energia mecânica é .
Passo 1
Qual vai ser a diferença entre os dois casos?
A energia mecânica é a energia total do sistema, dada por:
Então, quando a partícula atinge uma posição de energia potencial igual ao valor de energia total , o que acontece?
Toda sua energia está na forma de e não tem mais nenhuma energia restante na forma de energia cinética .
Então, em um gráfico com a concavidade para cima (barriguinha para baixo) como esse, no trecho central:
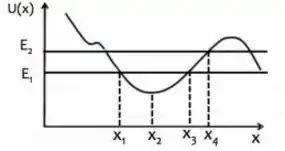
Os pontos e serão os pontos de retorno quando a partícula apresenta uma energia , enquanto o ponto será um dos dois pontos de retorno quando a partícula apresenta uma energia .
Esses pontos são chamados de pontos de retorno porque são os pontos onde a partícula para e começa a percorrer o caminho de volta, através da ação da força conservativa associada à energia potencial .
Por último, ainda podemos relacionar a força sobre a partícula com o gráfico de com:
A força é menos a derivada do gráfico de energia potencial . Ou seja, ela apresenta o valor da inclinação do gráfico, porém com o sinal negativo.
Vamos às alternativas...
Passo 2
(a) Quando a partícula está na posição a força sobre ela é a mesma nos dois casos.
Como já vimos no Passo 1, a força sobre a partícula é menos a derivada do gráfico da energia potencial :
Ela só depende da inclinação do gráfico, então, em um mesmo ponto , a partícula terá uma força igual independente de seu valor de energia mecânica.
A alternativa (a) está correta.
Passo 3
(b) Quando a partícula está na posição a sua velocidade é a mesma nos dois casos.
Na posição , a partícula terá o mesmo valor de energia potencial para os dois casos.
Entretanto, como a energia mecânica é maior no caso 2:
A parcela de energia restante na forma de cinética será maior no caso 2 também:
Então, a partícula passa no ponto com uma velocidade maior quando sua energia total vale .
A alternativa (b) está incorreta.
Passo 4
(c) Em ambos os casos, a posição é um ponto de retorno.
Como vimos no Passo 1, o ponto será ponto de retorno apenas quando a energia total for igual a . Pois nesse caso, toda a energia estará na forma de potencial , não sobrando nenhuma parcela na forma de energia cinética .
Já quando a energia total vale , no ponto ainda resta uma parcela da energia na forma de cinética, então a partícula ainda tem uma velocidade e vai passar desse ponto, não sendo um ponto de retorno.
A alternativa (c) está incorreta.
Passo 5
(d) Na posição a força sobre a partícula é nula apenas no caso em que a energia mecânica é .
Como na posição o gráfico de apresenta uma inclinação diferente de zero (horizontal), isso significa que a força atuando sobre a partícula é não nula também, independente de seu valor total de energia .
Assim, em ambos os casos teremos uma força atuando sobre a partícula no ponto .
A alternativa (d) está incorreta.
Passo 6
(e) A posição é uma posição em que a energia cinética é máxima, no caso em que a energia mecânica é .
No caso em que a energia mecânica é , a partícula nem chega a atingir o ponto , pois não tem energia suficiente para passar do ponto .
Já no caso em que a partícula tem energia igual a , podemos ver que a energia potencial em tem exatemente o valor da energia total .
Assim, toda a energia da partícula estará na forma de energia potencial e não sobra nenhuma parcela de energia cinética .
Logo, é mínima no ponto .
A alternativa (e) está incorreta.
Resposta
Letra (a)