Considere que um corpo percorrendo uma trajetória retilínea no sentido positivo do eixo , cuja energia potencial em função de é mostrada na figura abaixo, tenha, em , energia cinética igual a .

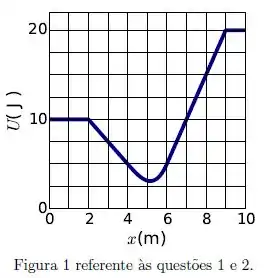
O ponto de retorno do corpo se encontra no intervalo:

O ponto de retorno é o ponto onde o corpo possui apenas energia potencial e nenhuma cinética (onde a energia total coincide com a curva da energia potencial, fazendo o corpo ter velocidade zero logo antes de mudar o sentido da sua velocidade).

Em a energia cinética do corpo é e, pelo gráfico, a energia potencial é . A energia total então é:

No gráfico, cada unidade no eixo vertical corresponde a ( Observe que do ao tem 4 unidades, o que dá cada unidade ).

Ou seja, a nossa energia cinética está próxima de no gráfico. Rebatendo na curva de energia potencial, o ponto de retorno está no intervalo:

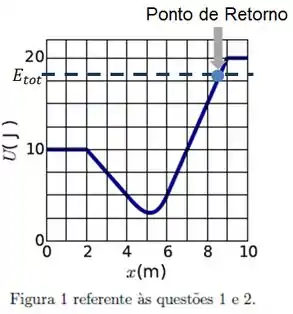
Que corresponde à letra (b)