Halliday - Vol.1 - Ed. 8 - Capítulo 7 – Problemas Adicionais – Questão 54
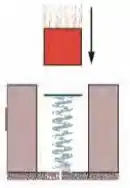
(Capítulo 7 – Problemas Adicionais – Exercício 54) Um bloco de é deixado cair em uma mola vertical, inicialmente relaxada, cuja constante elástica é (Fig. 7-44). O bloco fica acoplado à mola, comprimindo-a em até parar momentaneamente. Nessa compressão, que trabalho é realizado sobre o bloco (a) pela força gravitacional e (b) pela força elástica? (c) Qual é a velocidade do bloco imediatamente antes de se chocar com a mola? (d) Se a velocidade no momento do impacto é duplicada, qual é a compressão máxima da mola?
Passo 1
Faaala galera, tudo certinho? Vamos lá pra mais uma!!
Devemos perceber para iniciar esse exercício que somente duas forças atuam sobre a caixa, uma força constante (força peso) e uma variável (força elástica), porém, ambas são conservativas e, por isso, podemos calcular o trabalho aplicando o seguinte teorema:
Ou seja, o trabalho realizado por uma força conservativa é igual a menor a variação da energia potencial associada a esta força. Lembrando que:
Devemos perceber também que as unidades dessa questão estão fora do SI, portanto, no decorrer da questão usaremos alguns fatores de conversão para converter tudo para o SI, show?
Passo 2
Calculando o trabalho realizado pelo peso durante a compressão da mola, considerando que nossa cota de altura igual a zero vai ser no ponto de compressão máxima da mola, ou seja, . Assim:
Passo 3
De maneira análoga, vamos aplicar o mesmo teorema para a força elástica, considerando :
Passo 4
Para determinar a velocidade com que o bloco atinge a mola, vamos aplicar o teorema trabalho-energia cinética durante a compressão. Como na compressão máxima a velocidade é nula, então, , assim:
Como já calculamos os trabalhos realizados pela força elástica e pela força peso, então, substituindo os valores:
Isolando :
Passo 5
Para determinarmos a compressão máxima quando a velocidade é duplicada, faremos o processo que fizemos nos passos anteriores, porém, ao contrário. Assim, escrevendo o teorema trabalho-energia cinética, para uma velocidade duas vezes maior do que a velocidade calculada:
Passo 6
Escrevendo agora os trabalhos da força peso e da força elástica em função da nova compressão , usando as mesmas considerações anteriores:
Passo 7
Substituindo a e a na :
Resolvendo esta equação do segundo grau, encontramos:
Porém, nosso deslocamento deve ser positivo devido as considerações feitas, assim:
Resposta
- ;
- ;
- ;
- .