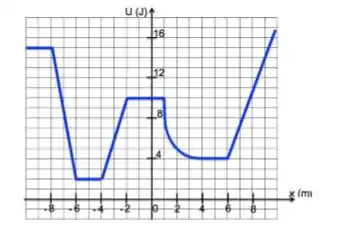
Considere uma partícula de massa que pode se mover somente ao longo do eixo , sujeita a apenas uma força conservativa , nessa direção, com energia potencial representada no gráfico abaixo. Não existem forças dissipativas. Inicialmente a partícula se encontra na origem, movendo-se no sentido negativo de , com velocidade . O trabalho realizado pela força quando a partícula se desloca de um ponto até um ponto é denotado por .
Assinale a alternativa correta:
(a) Em e.
(b)
(c) Em , e .
(d)
(e) Em , e .
(f) Em , e .
(g) Em , e independe de .
(h) Em , e .
Passo 1
Analisando cada uma das alternativas, temos:
a) Quando , a energia cinética é dada por:
Já a energia potencial inicial é, de acordo com o gráfico:
Para , temos que a inclinação da reta é positiva, portanto:
E a força então é negativa.
Já para saber sobre o módulo da velocidade neste ponto, acharemos antes a energia potencial desse ponto, que de acordo com o gráfico é:
Portanto, foram convertidos da energia potencial inicial para energia cinética, logo:
A alternativa está errada.
Passo 2
b) Vamos calcular cada um dos trabalhos apresentados:
E o outro:
Logo:
Portanto, a alternativa está errada.
Passo 3
c) A força que age no ponto pode ser calculada da seguinte maneira:
Como no ponto o gráfico da energia potencial é uma constante, temos que:
Já para a segunda parte da alternativa, iremos encontrar a energia potencial da partícula no ponto , que nos gráfico nos diz que:
Portanto, a diferença de da condição inicial é uma evidência que esta energia foi convertida para energia cinética, logo:
A alternativa está errada
Passo 4
d) Vamos calcular cada um dos trabalhos apresentados:
E o outro:
Portanto, a alternativa está errada.
Passo 5
e) Para , vemos que a inclinação da reta é positiva, portanto:
Já a energia potencial da partícula neste ponto é, segundo o gráfico:
Portanto, a diferença de da condição inicial é uma evidência que esta energia foi convertida para energia cinética, logo:
A alternativa está errada.
Passo 6
f) Em , temos que a inclinação do gráfico é positiva, portanto:
Já a energia potencial da partícula neste ponto, segundo o gráfico é:
Portanto, a diferença de da condição inicial é uma evidência que esta energia foi convertida para energia cinética, logo:
A alternativa está correta.
Passo 7
g) A afirmação que independe de é inconsistente, visto que altera a energia inicial e consequentemente toda a energia armazenada no sistema. A afirmativa é falsa.
Passo 8
h) Esta é uma negação da alternativa certa, a letra (f).
Resposta
(f)