Uma partícula de massa está submetida a um campo de força conservativa em uma dimensão conforme o gráfico abaixo. A energia potencial nesse campo, :
- É constante e igual a para ;
- Decresce linearmente entre e, onde seu valor é (trecho linear);
- Permanece constante entre e (trecho constante);
- É dada por: para (trecho parabólico);
Sendo a partícula abandonada em repouso no ponto :
- Calcule a energia mecânica da partícula e superponha seu gráfico como função
de ao gráfico do potencial.
b) Calcule o máximo valor de alcançado pela partícula em seu movimento subsequente
e indique no gráfico.
c) Obtenha a expressão para a energia cinética em função de e faça seu gráfico no espaço
apropriado entre os limites inferior e superior que a partícula pode atingir.
d) Obtenha a expressão e faça o gráfico da componente da força que age sobre a partícula
devido a esse potencial em função da posição entre os limites inferior e superior que a partícula
pode atingir.
e) Suponha agora que, ao ser abandonada a partícula nesse campo, seja adicionada uma
força de atrito de módulo constante , contrária ao movimento (por exemplo, atrito
com uma superfécie paralela ao eixo x). Faça o gráfico de para esta nova situação (superposto ao de U(x)), e determine o novo valor máximo de alcançado pela partícula.
Passo 1
a)
Ah, a gente sabe que a energia mecânica pode ser calculada da seguinte forma:
No finalzinho da questão ele diz que a partícula é abandonada do repouso em .Ele quis dizer com isso que em ele vai estar com velocidade nula e consequentemente energia cinética também nula. Assim, só vai restar...
Mas e aí, como que acharemos o U ?
Passo 2
Vamos ter que usar métodos mais matemáticos que físicos agora. Lááá em tempos não tão remotos, ensino médio e tal, quando se estudou Geometria Analítica nos pediam para calcular a equação da reta de um gráfico só dando os pontos iniciais e finais da equação. Bem, aqui temos os pontos iniciais e finais e entre eles terá um gráfico linear. Para calcular o potencial em é só achar essa equação e substituir em U (-40).
Os pontos são: (-50,2000) e (-20, -1000).
Utilizando a fórmula para determinar a equação da reta, teremos:
Esse nosso pode ser calculado por:
Substituindo o ponto (-50,2000), teremos:
Agora, achando , vamos achar...
Passo 3
O gráfico será constante em 2000J antes de , cairá linearmente com a equação entre e , permanecerá constante em -1000J até e subirá, para valores de como parábola de função , como no gráfico abaixo:
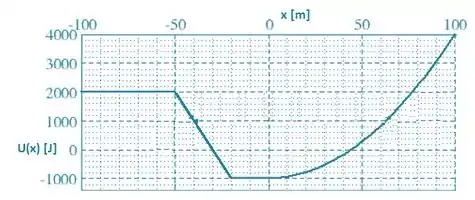
Passo 4
b)
O valor de será aquele em que o potencial será igual a energia mecânica total, já que não podemos ter energia cinética negativa. Assim, teremos que:
Passo 5
c)
Como falei no Passo 4 a energia cinética SEMPRE deve ser positiva, então só haverá energia cinética em pontos em que o gráfico do potencial está abaixo de 1000J, nesse caso, haverá energia cinética no intervalo .
Também vimos lá no Passo 1 que , logo:
Como a gente já viu que e também já achamos todas as equações de U, teremos:
O gráfico ficará mais ou menos assim:
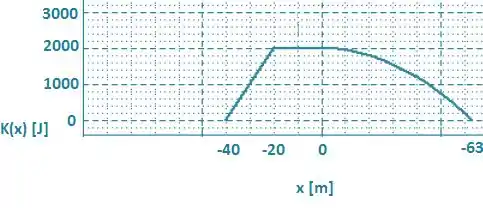
Passo 6
d)
Existe alguma relação do potencial com a força ? SIM! E é bem simples:
Para cada trecho teremos uma força. Bora lá:
[Parte da Parábola]
[Partes Constantes]
Derivada de constante é nula, então:
[Parte Linear]
Obs:NÃO ESQUECE DO SINAL DE MENOS NAS DERIVADAS!!
Ah, esse seria o gráfico da força.
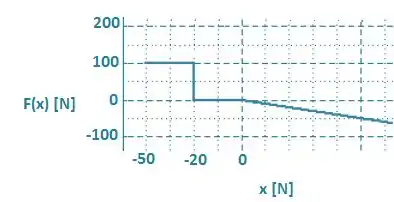
Passo 7
e)
Simbora, galera! Só falta mais essa pra acabar!!
O nosso querido amigo autor da questão nos pediu pra fazer o gráfico dessa nova situação aí. A diferença é que a energia mecânica não se conservará, será sendo subtraído o trabalho da força de atrito. Desta forma, teremos:
Para ter trabalho da força de atrito, precisamos que o corpo esteja em movimento, como ele nos disse no enunciado, quando ele entra em movimento, logo podemos considerar o nosso .
Substituindo os valores que a gente sabe, vamos ter:
Passo 8
O valor de é o valor que que é quando o potencial não poderá crescer mais devido o trabalho que foi gasto pelo trabalho da força de atrito. Ou seja, a energia mecânica vai ter decrescido até certo ponto que o potencial não poderia mais aumentar.
Plotando os gráficos sobrepostos, teremos:
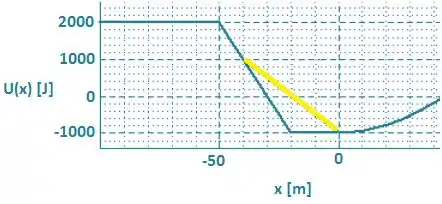
Podemos notar graficamente que em tanto quanto valem -1000J, desta forma .
Poderíamos encontrar isso também algebricamente, escrevendo as fórmulas do potencial e da energia mecânica e igualando.
ou , que não vale pra essa questão, já que o potencial máximo está em Assim:
Resposta
e)