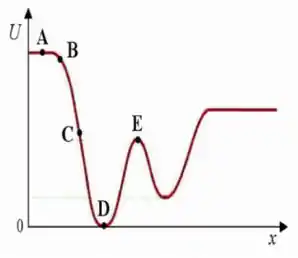
O gráfico abaixo mostra a energia potencial em função da distância de um objeto em movimento ao longo do eixo x. Em qual dos pontos marcados a força que age sobre o objeto tem a maior módulo?
a) ponto A
b) ponto B
c) ponto C
d) ponto D
e) ponto E
Passo 1
Que belezura de gráfico, hein?
Bom, olha aí, esse é um gráfico da Energia Potencial pela distância. Esse gráfico tem uma característica legal, que é: a força conservativa que atua no corpo dita a inclinação do gráfico. Ou em outras palavras:
Ou seja, a força é igual a menos a derivada da energia potencial pela distância.
Como nós queremos o maior módulo, então não importa se a força é positiva ou negativa, o que importa é o quão inclinado o gráfico está.Dá uma olhada no gráfico. Em A, D e E, a força é 0, pois a derivada é 0. Sobrou B e C, só que em C, a inclinação é maior do que em B. Logo, a resposta correta é a letra c).
Resposta
Letra c)