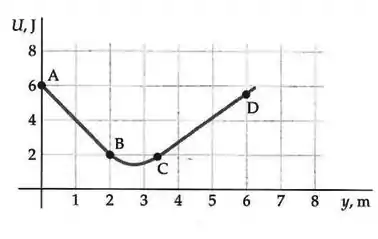
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força , cuja energia potencial associada, , está representada no gráfico ao lado. Os trechos e s’ao retos. A energia da partícula é . Quando a partícula passa pela posição , sua rapidez e a força sobre ela valem
(a) ;
(b) ;
(c) ;
(d) ;
(e) ;
Passo 1
Quando a partícula está no trecho , e nesse trecho podemos calcular a força por meio de
Pra calcular essa derivada podemos calcular a inclinação da reta , assim
Passo 2
Olhando o gráfico vemos que a energia potencial é
E o enunciado nos diz que a energia mecânica é
Assim podemos relacionar energia mecânica com a potencial e a cinética
Agora podemos calcular a velocidade da partícula
Resposta
(A)
Exercícios de Livros Relacionados
Uma única força conservativa F ( x ) age sobre uma partícula de 1,0k g que se move ao longo de um eixo x . A energia potencial U ( x ) associada a F ( x ) é dada por U x = - 4 x e - x 4J onde x está e
A energia potencial entre dois átomos de hidrogênio separados por uma distância x muito grande é dada por U x = - C 6 / x 6 , onde C 6 é uma constante positiva. Qual é a força que um átomo exerce sobr
Duas massas, m 1 e m 2 , estão sobre o eixo x, sendo m1 mantido no lugar de origem e m 2 naposição x, livre para se mover. A energia potencial gravitacional dessas massas é dada por U x = - G m 1 m 2
A massa do Ônibus Espacial orbital é cerca de 8 × 10 4k g e o período de sua órbita é 90 min. Estime a energia cinética da nave e o trabalho realizado pela gravidade sobre ela entre o lançamento e a e
A força atrativa entre dois núcleons (prótons ou nêutrons) é descrita com boa aproximação pelo potencial de Yukawa V r = - V o r o r e - r r o Onde V o = 8,0x10 - 12 J ,r o = 1,5x10 - 15m e r é a dist