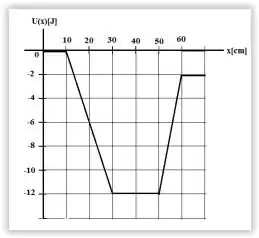
Uma partícula de massa 1,00 kg move-se ao longo do eixo x na região em que a energia potencial U(x) varia conforme a figura. Quando a partícula se encontra em x =20,0 cm, sua velocidade é de -2,00 m/s.

Determine o intervalo onde ocorre o movimento da partícula.

A) 12 ≤ x(cm) ≤ 60

B) 20 ≤ x(cm) ≤ 55

C) 16 ≤ x(cm) ≤ 57

D) 23 ≤ x(cm) ≤ 54

E) 16 ≤ x(cm) ≤ 24

Vamos usar aqui a conservação da energia mecânica.

Sabemos que o somatório da energia cinética com a energia potencial se conserva:

Vamos calcular a energia mecânica total da partícula de acordo com o que foi fornecido no momento em que ela se encontra no ponto .

Temos uma energia cinética de:

A energia potencial, podemos achar pelo gráfico e vale:

Assim, a energia mecânica total vale:

Repare que não existe energia cinética negativa. Então, para qualquer valor de energia potencial maior do que a partícula estará em repouso.

Assim, sabemos que o movimento da partícula ocorre quando a energia potencial dela é menor do que .

Olhando para o gráfico, isso acontece de 16 cm até 57 cm.