Uma partícula de massa se movendo no eixo está sujeita a uma única força, cuja energia potencial é dada na figura abaixo. Quando passa pela posição , a velocidade da partícula é .
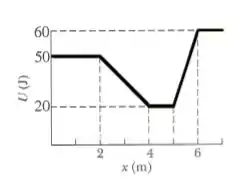
(a) Qual é o módulo e o sentido da aceleração da partícula no ponto ?
(b) A partícula chega ao ponto ? Em caso afirmativo, qual é a velocidade da partícula nesse ponto? Caso contrário, qual é o ponto de retorno entre e ?
(c) Considere agora que a partícula se move de até . Qual é o trabalho realizado pela força?
Passo 1
a) Aqui nós devemos usar a relação da força em uma direção com a variação da energia potencial.
Para encontrar a aceleração:
Como a aceleração aponta no sentido positivo do eixo
Passo 2
b) Pela conservação da energia mecânica, temos:
Como a energia potencial do ponto é de , a partícula com apenas de energia não alcançará tal ponto.
Para encontrar o ponto de retorno, basta fazermos que . Com isso teremos que:
E então:
Multiplicando cruzado e resolvendo:
Portanto:
Passo 3
c) Sabemos que:
Logo:
Resposta
a)
b)
c)