Um potencial unidimensional é mostrado na figura abaixo. Uma partícula sujeita a este potencial tem energia mecânica total E. Assinale a alternativa incorreta.

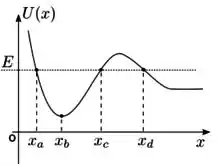
1. A força agindo no ponto é negativa.
2. A velocidade da partícula se anula em
3. A força agindo na partícula no ponto é nula.
4. A energia cinética da partícula é máxima entre e
5. A posição é um ponto de retorno.

a):

Bom, como a derivada de ali é positiva, já que a inclinação da curva também é, então, o sinal da força vai ser negativo mesmo:

Verdadeira.

b):

Como o sistema tem uma energia total ,a partícula não pode passar dali. Isso quer dizer que ali é um ponto de retorno.

Isso quer dizer...que sim, a velocidade se anula ali. Velocidades se anulam em pontos de retorno.

Imagine a partícula efetuando um movimento ali naquela “vala”, entre e . Ela vai ficar indo e vindo, e quando atingir um ponto, mudará de direção, logo, pra que isso aconteça, a velocidade precisa primeiro se anular.

Verdadeira.

c):

Como a derivada ali é zero:

Verdadeira.

d):

Isso ta errado....por quê?

Bom, o enunciado diz que a energia mecânica máxima do sistema é

Então a partícula não pode entrar naquela região entre e

Assim:

Falsa.

e):

Como é um ponto de energia potencial máxima e dali a partícula não pode passar( considerando que ela esteja vindo de , então, é sim um ponto de retorno.

Verdadeira.

Então:

d)