Origem do Exercício
Um corpo descreve um movimento retilíneo ao longo do eixo sob ação de uma única força conservativa. O gráfico da energia potencial do corpo em função de é mostrado na figura .
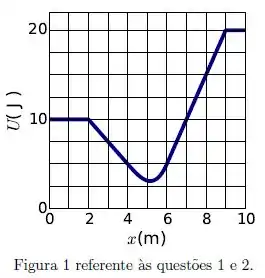
Pode-se concluir que a componente da força que age sobre o corpo em é igual a:
Passo 1
Podemos obter a componente da força conservativa pela derivada da energia potencial com relação àquele eixo.
Isso significa que a força é a tangente à nossa curva multiplicada por . Em , temos um trecho aproximadamente reto, e podemos calcular essa tangente:
Pelo gráfico, os pontos aparentemente mais fáceis de usar são correspondendo a e correspondendo a .
Que é a letra (e).
Resposta
Letra (e)
Exercícios de Livros Relacionados
Uma única força conservativa F ( x ) age sobre uma partícula de 1,0k g que se move ao longo de um eixo x . A energia potencial U ( x ) associada a F ( x ) é dada por U x = - 4 x e - x 4J onde x está e
A energia potencial entre dois átomos de hidrogênio separados por uma distância x muito grande é dada por U x = - C 6 / x 6 , onde C 6 é uma constante positiva. Qual é a força que um átomo exerce sobr
Duas massas, m 1 e m 2 , estão sobre o eixo x, sendo m1 mantido no lugar de origem e m 2 naposição x, livre para se mover. A energia potencial gravitacional dessas massas é dada por U x = - G m 1 m 2
A massa do Ônibus Espacial orbital é cerca de 8 × 10 4k g e o período de sua órbita é 90 min. Estime a energia cinética da nave e o trabalho realizado pela gravidade sobre ela entre o lançamento e a e
A força atrativa entre dois núcleons (prótons ou nêutrons) é descrita com boa aproximação pelo potencial de Yukawa V r = - V o r o r e - r r o Onde V o = 8,0x10 - 12 J ,r o = 1,5x10 - 15m e r é a dist